Channel with a finite memory
A communication channel for which the statistical properties of the output signal at a time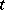 
are determined by the input signals transmitted at the times 
, 
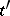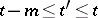(and therefore do not depend on the signals transmitted prior to the time 
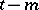); the number 
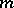is called the size (or length) of the memory of the channel.
More precisely, a discrete-time communication channel where the input and output signals are given, respectively, by random sequences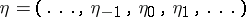 
and 
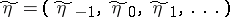with values in the spaces 
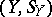and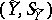 
is called a channel with a finite memory if a compatible set of conditional distributions
 |
by means of which such a channel can be defined, satisfies for any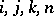 
, and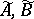 
the conditions
 |
 |
 |
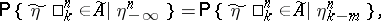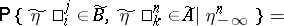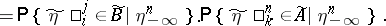Here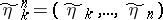 
, 
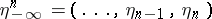, and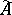 
(respectively, 
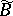) is a set in the direct product of 
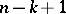(respectively, 
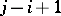) copies of 
. A continuous-time channel with a finite memory is defined similarly.
References
| [1] | A.Ya. Khinchin, "On the basic theorems of information theory" Uspekhi Mat. Nauk , 11 : 1 (1956) pp. 17–75 (In Russian) |
| [2] | A.A. Feinstein, "Foundations of information theory" , McGraw-Hill (1968) |
| [3] | J. Wolfowitz, "Coding theorems of information theory" , Springer (1964) |
Channel with a finite memory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Channel_with_a_finite_memory&oldid=46304