Cayley form

A form in 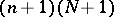variables, where 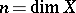, with 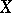a closed algebraic subvariety of an 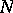-dimensional projective space 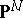, which is determined by 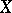uniquely up to a constant factor and itself uniquely determines 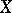. The exact definition is as follows. Let 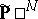be the 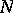-dimensional projective space of all hyperplanes in 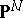, and let 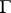be the subset of the variety

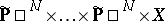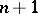( factors ) consisting of all -tuples 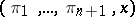, where 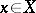is a point in the intersection of the hyperplanes 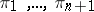and

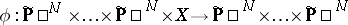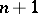( factors each time) is the natural projection. Then 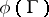is an irreducible subvariety of codimension 1 in

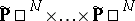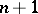( factors) and so 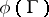is the zero variety for some form 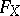on

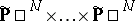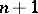( factors).

It may always be assumed that 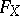has no multiple factors, and this condition defines 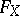uniquely up to multiplication by a constant, given 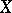. Conversely, 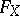uniquely determines the set of all possible 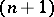-tuples of hyperplanes in 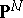that intersect at points of , and so 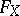uniquely determines . The form 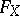is called the Cayley form of .

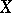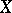The Cayley form is also frequently known as the Chow form, or the associated form, of the variety . The idea of defining by the complex of linear subspaces of dimensio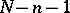n in that intersect 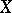goes back to A. Cayley [5], who applied it to the case 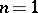, 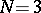. The coefficients of the Cayley form are known as the Chow coordinates of the variety .

The Cayley form 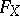is homogeneous in each of the 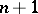coordinate systems of the space

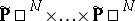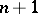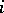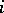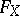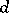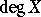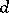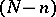( factors) (the -th coordinate system is the coordinate system of the -th factor in this space). The form has the same degree of homogeneity with respect to each system; this common degree is denoted by and is called the degree of the subvariety . It admits a geometrical interpretation: is the maximum number of points of intersection of with all possible -dimensional linear spaces 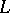in 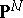such that 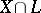is a finite set (i.e. 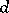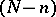is the number of points in the intersection of with a "general" -dimensional linear subspace).

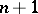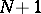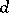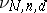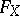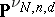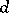The set of all forms (up to multiplication by a non-zero constant) in groups of variables consisting of variables and having degree in each group, forms a projective space of dimension . The Cayley form may be identified with a point of . The set of all points in which are Cayley forms of -dimensional closed subvarieties of degree in 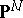is a quasi-projective variety; it parametrizes the family of all such subvarieties in such a way that the family is algebraic relative to the parametrization. In general, 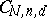need not be closed in .

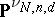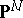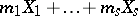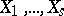The construction of the Cayley form carries over in a natural way to closed -dimensional cycles in , i.e. to formal linear combinations of closed -dimensional subvarieties in 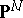with integer coefficients . In fact, one puts

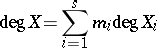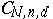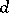and . The set of all Cayley forms of -dimensional cycles of degree in 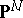is closed in .

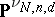The investigation of Cayley forms and the properties of the varieties 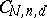and 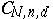constitute an important aspect in the problem of classifying subvarieties and cycles in . The first stage in this classification is to study the decomposition of 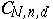into irreducible components. For example, if 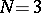, , 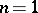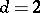(curves of degree 2 in three-dimensional space), the variety 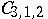decomposes into two irreducible 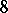-dimensional components. The first corresponds to planar curves of the second order, the second to pairs of straight lines. The birational classification of the varieties 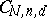is an important problem (in all known examples these varieties are rational).

References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001
[2]	W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1952) MR0048065 Zbl 0048.14502
[3]	P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1955) MR0072531
[4]	W.-L. Chow, B.L. van der Waerden, "Zur algebraische Geometrie IX" Math. Ann. , 113 (1937) pp. 692–704 Zbl 0016.04004
[5]	A. Cayley, "On a new analytical representation of curves in space" , Collected mathematical papers , 4 , Cambridge Univ. Press (1891) pp. 446–455 (Quart. J. Pure Appl. Math. 3 (1860), 225–236)

Comments

The varieties 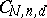are special cases of Hilbert schemes (cf. Hilbert scheme).