Cayley-Klein parameters

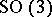Special coordinates in the rotation group of three-dimensional space, the construction of which is based in the final analysis on the relationship between and the group of unitary matrices with determinant 1. There exists a mapping which is an epimorphism by virtue of its algebraic properties and a double covering by virtue of its topological properties. (Restricted to some neighbourhood of the identity matrix, is an isomorphism; in other words, and are locally isomorphic.) Each matrix may be written as

where are complex numbers such that 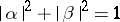. These are taken to be the Cayley–Klein parameters of 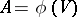. (The term is sometimes used for all four elements of the matrix 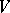.) As the actual construction of a mapping 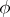with the above properties may be accomplished in various ways, different authors define the Cayley–Klein parameters in slightly different ways (see [2], [3]).

Since 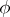is not a true isomorphism, but only a double covering, it is impossible to define the Cayley–Klein parameters as (continuous) coordinates on all of ; this can be done only locally. However, the Cayley–Klein parameters may nevertheless be used to study processes of rotation in which 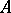is a continuous function of a real parameter (and there is no necessity to restrict the domain of possible values of in any way). Indeed, if some fixed value has been chosen at , the corresponding values of are uniquely defined by continuity for all 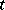. (The fact that the complete inverse is double-valued intrudes only in the observation that not only when but also when 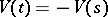.) Thus the Cayley–Klein parameters can be applied to investigate the motion of a rigid body with a fixed point (the configuration space of which is ). This approach was adopted in [1], but did not achieve popularity.

The group is isomorphic to the group of quaternions with norm 1 (cf. Quaternion); hence, by going over from 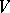to the corresponding quaternion , one can replace the Cayley–Klein parameters by the Euler–Rodriguez parameters — four real numbers such that . These stand in a simple relationship to the Cayley–Klein parameters (see [1], [3]) and possess the same "double-valuedness" property (for the history of the problem see [1]). It was essentially in this context that attention was first directed to two-valued representations of the rotation group (see Spinor).

References

[1]	F. Klein, A. Sommerfeld, "Ueber die Theorie des Kreises" , 1–2 , Teubner (1965)
[2]	H. Goldstein, "Classical mechanics" , Addison-Wesley (1953)
[3]	J.L. Synge, "Classical dynamics" , Handbuch der Physik , 3/1 , Springer (1960) pp. 1–225

References

[a1]	P. Du Val, "Homographies, quaternions and rotations" , Clarendon Press (1964)