Cascade method

Laplace method

A method in the theory of partial differential equations enabling one, in some cases, to find the general solution of a linear partial differential equation of hyperbolic type,

(1)

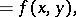by constructing a sequence of equations

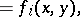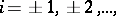such that the solution of (1) is expressed in terms of the solutions of the latter.

Equation (1) can be written in one of the following forms:

where

The functions 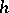and are called invariants of (1).

When 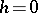, solving (1) reduces to the integration of ordinary differential equations, and its solution has the form:

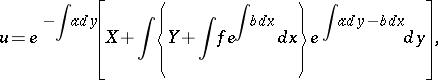where and 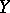are arbitrary functions of and 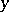, respectively. Similarly, if 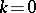, the solution of (1) can be written in the form

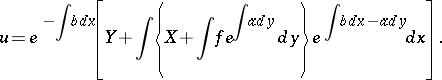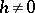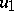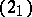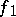In case , the solution to (1) can be obtained from the solution of whose coefficients and right-hand side have the form

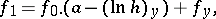by means of the formula

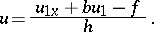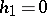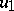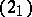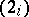If , the solution of is obtained by the above method; if , the process is further continued by constructing equations for 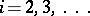; the solution of (1) is expressed by means of quadratures in terms of the solutions of this sequence of equations. For the case 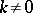, a chain of equations can similarly be constructed for 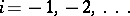. If at some stage 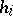(or 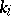) vanishes, then the general solution to (1) is obtained in quadratures.

The cascade method can be used to pass from a given equation to an equation for which some other known analytic or numerical method of solution is more easily applied; for obtaining families of equations whose solutions are known and whose coefficients closely approximate those of the equations encountered in important applied problems; and finally for obtaining fundamental operators in perturbation theory of operators.

The cascade method was discovered by P. Laplace [1] in 1773 and developed by G. Darboux [2].

References

[1]	P.S. Laplace, , Oeuvres complètes , 9 , Paris (1893) pp. 5–68
[2]	G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) pp. 1–18
[3]	F.G. Tricomi, "Lectures on partial differential equations" , Moscow (1957) (In Russian; translated from Italian)
[4]	V.M. Babich, et al., "Linear equations of mathematical physics" , Moscow (1964) (In Russian)
[5]	G.A. Dombrovskii, "The method of adiabatic approximation in the theory of plane gas flows" , Moscow (1964) (In Russian)
[6]	T.V. Chekmarev, "Generalized model systems of mixed-type equations" Izv. Vuzov. Mat. , 11 (1972) pp. 72–79 (In Russian)
[7]	V.I. Pashkovskii, "Related operators and boundary-value problems for elliptic equations" Differential Eq. , 12 : 1 (1977) pp. 81–88 Differentsial'nye Uravneniya , 12 (1976) pp. 118–128