Carnot theorem
A theorem on the product of the simple ratios in which the points of intersection of an algebraic curve with the sides of a triangle divide these sides. Suppose that the algebraic curve 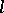 of order
of order  does not pass through any of the vertices of a triangle
does not pass through any of the vertices of a triangle 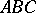 and intersects each side, extended if necessary, at
and intersects each side, extended if necessary, at  points: the side
points: the side 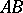 at the points
at the points 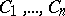 ; the side
; the side  at the points
at the points 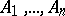 ; and the side
; and the side  at the points
at the points 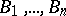 . Then the product of the
. Then the product of the  simple ratios
simple ratios
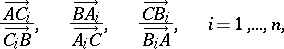 |
is equal to 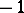 if
if  is odd, and
is odd, and 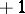 if
if  is even.
is even.
This statement is equivalent to the following: The product of the 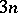 ratios
ratios
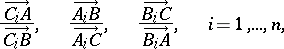 |
is equal to 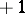 .
.
A special case of this theorem was proved by L. Carnot [1].
If 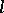 is a straight line then the Menelaus theorem is obtained. A generalization of Carnot's theorem is: Suppose that an algebraic curve of order
is a straight line then the Menelaus theorem is obtained. A generalization of Carnot's theorem is: Suppose that an algebraic curve of order  intersects each of the straight lines
intersects each of the straight lines  ,
, 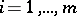 ,
, 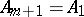 , lying in the plane of this curve, at exactly
, lying in the plane of this curve, at exactly  points
points 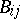 ,
, 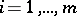 ;
; 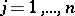 . Then
. Then
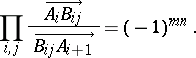 |
References
| [1] | L. Carnot, "Géométrie de position" , Paris (1803) |
Carnot theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carnot_theorem&oldid=46259