Carlson inequality
From Encyclopedia of Mathematics
Let 
be non-negative numbers, not all zero. Then
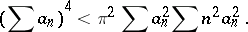 | (1) |
Proved by F. Carlson [1]. The analogue of the Carlson inequality for integrals is: If 
, 
, then
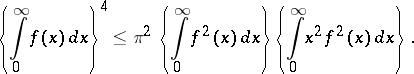 | (2) |
The constant 
is best possible in the sense that there exists a sequence 
such that right-hand side of (1) is arbitrarily close to the left-hand side, and there exists a function for which (2) holds with equality.
References
| [1] | F. Carlson, "Une inegalité" Ark. Math. Astron. Fys. , 25B : 1 (1934) pp. 1–5 |
| [2] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
How to Cite This Entry:
Carlson inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carlson_inequality&oldid=46220
Carlson inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carlson_inequality&oldid=46220
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article