Carleson set

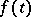A closed set on which every function defined and continuous on this set is representable by a series of the form , where 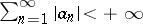. Introduced by L. Carleson [1]. Carleson sets form an important class of so-called thin sets (cf. Fine set; Thinness of a set). In order that a closed set be a Carleson set, it is necessary and sufficient that there exists a constant such that the Fourier–Stieltjes coefficients

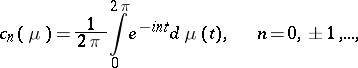of each measure 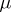concentrated on 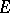satisfy the inequality

References

[1]	L. Carleson, "Sets of uniqueness for functions regular in the unit circle" Acta Math. , 87 : 3–4 (1952) pp. 325–345
[2]	I. Wik, "On linear dependence in closed sets" Arkiv. Mat. , 4 : 2–3 (1960) pp. 209–218
[3]	J.-P. Kahane, R. Salem, "Ensembles parfaits et séries trigonométriques" , Hermann (1963) pp. 142
[4]	J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970)

Comments

A closed set 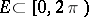is called a Helson set if every function 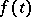defined and continuous on 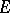is representable by a series of the form , where 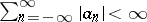; see [a1]. Obviously, every Carleson set is a Helson set. I. Wik proved the surprising result that, conversely, every Helson set is a Carleson set; see [2]. So the two notions amount to the same.

Using a technique of S.W. Drury, N.Th. Varopoulos proved in 1970 that the union of two Helson sets is again a Helson set; see [a2].

References

[a1]	H. Helson, "Fourier transforms on perfect sets" Studia Math. , 14 (1954) pp. 209–213
[a2]	N.Th. Varopoulos, "Sur la réunion de deux ensembles de Helson" C.R. Acad. Sci. Paris Sér. A-B , 271 (1970) pp. A251-A253