Carleman kernel
From Encyclopedia of Mathematics
A measurable, in general complex-valued, function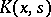 
satisfying the conditions: 1) 
almost-everywhere on 
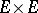, where 
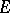is a Lebesgue-measurable set of points in a finite-dimensional Euclidean space; and 2) 
for almost-all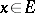 
.
References
| [1] | I.M. [I.M. Glaz'man] Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1980) (Translated from Russian) |
How to Cite This Entry:
Carleman kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleman_kernel&oldid=46208
Carleman kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleman_kernel&oldid=46208
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article