Carleman boundary value problem
A boundary value problem for analytic functions involving a shift which reverses the direction of traversing the boundary. It was first considered by T. Carleman [1]. Let 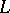 be a simple closed Lyapunov curve (cf. Lyapunov surfaces and curves) in the complex
be a simple closed Lyapunov curve (cf. Lyapunov surfaces and curves) in the complex  -plane and let
-plane and let 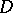 be the finite domain bounded by
be the finite domain bounded by 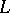 . Let
. Let 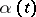 be a given complex-valued function on
be a given complex-valued function on 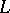 inducing a one-to-one mapping of
inducing a one-to-one mapping of 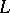 onto itself reversing the direction of traversing
onto itself reversing the direction of traversing 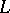 and satisfying additionally the Carleman condition:
and satisfying additionally the Carleman condition:
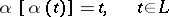 | (*) |
(it is further supposed that the derivative 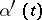 satisfies a Hölder condition). Then the Carleman boundary value problem consists in finding a function
satisfies a Hölder condition). Then the Carleman boundary value problem consists in finding a function  , analytic in
, analytic in 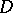 except for a finite number of poles, continuous on
except for a finite number of poles, continuous on 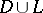 and subject to the boundary condition
and subject to the boundary condition
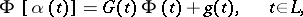 |
where the functions 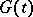 and
and 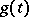 given on
given on 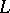 satisfy a Hölder condition and
satisfy a Hölder condition and 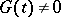 on
on 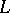 .
.
The Carleman boundary value problem has also been studied under the condition
 |
which is more general than (*), and so has the Carleman boundary value problem for several unknown functions (see [2], [3]).
References
| [1] | T. Carleman, "Sur la théorie des équations intégrales et ses applications" , Verh. Internat. Mathematiker Kongress. Zürich, 1932 , 1 , O. Füssli (1932) pp. 138–151 |
| [2] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1977) (Translated from Russian) |
| [3] | N.P. Vekua, "Systems of singular integral equations and some boundary value problems" , Moscow (1970) (In Russian) |
Carleman boundary value problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleman_boundary_value_problem&oldid=46207