Carathéodory-Fejér problem

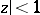The problem of extending a polynomial in to a power series representing a regular function in the disc which realizes the least value of the supremum of the modulus on the disc 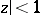in the class of all regular functions in the unit disc having the given polynomial as initial segment of the MacLaurin series. The solution to this problem is given by the following theorem.

Carathéodory–Fejér theorem [1]. Let

be a given polynomial, 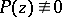. There exists a unique rational function 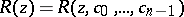of the form

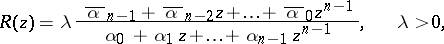regular in the unit disc and having 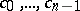as the first coefficients of its MacLaurin expansion. This function, and only this, realizes the minimum value of

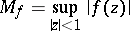in the class of all regular functions 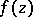in the unit disc of the form

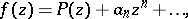and this minimum value is .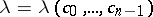

The number 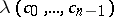is equal to the largest positive root of the following equation of degree :

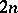If 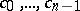are real, then 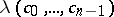is the largest of the absolute values of the roots of the following equation of degree :

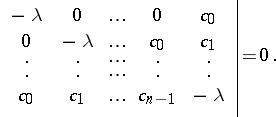References

[1]	C. Carathéodory, L. Fejér, "Ueber den Zusammenhang der Extremen von harmonischen Funktionen mit ihren Koeffizienten und den Picard–Landau'schen Satz" Rend. Circ. Mat. Palermo , 32 (1911) pp. 218–239
[2]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)