Canonical set
closed, 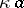 -set
-set
A set 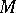 of a topological space which is the closure of an open set; in other words, it is the closure of its own interior
of a topological space which is the closure of an open set; in other words, it is the closure of its own interior 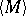 :
: 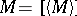 . Every closed set
. Every closed set 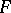 contains a maximal
contains a maximal 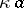 -set, namely
-set, namely 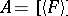 . The union of two
. The union of two 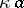 -sets is a
-sets is a 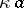 -set, but their intersection need not be. A set which is a finite intersection of
-set, but their intersection need not be. A set which is a finite intersection of 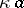 -sets is called a
-sets is called a 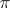 -set.
-set.
A set which is the interior of a closed set is called a canonical open set or 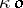 -set; in other words, it is a set which is the interior of its own closure:
-set; in other words, it is a set which is the interior of its own closure: 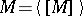 . Every open set
. Every open set 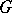 is contained in a smallest
is contained in a smallest 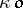 -set, namely
-set, namely 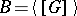 . Open canonical sets can also be defined as complements of closed canonical sets, and vice versa.
. Open canonical sets can also be defined as complements of closed canonical sets, and vice versa.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Comments
Other terms for canonical set are: regular closed set or closed domain. Canonical open sets are also called regular open sets or open domains.
In the Russian literature 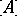 denotes the closure of
denotes the closure of 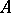 and
and 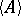 the interior of
the interior of 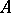 . In Western literature these are denoted by
. In Western literature these are denoted by 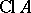 and
and 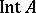 , respectively.
, respectively.
The collection of regular closed sets forms a Boolean algebra under the following operations 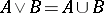 ,
, 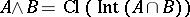 and
and 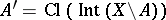 . The same can be done for the collection of regular open sets.
. The same can be done for the collection of regular open sets.
If 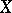 is a compact Hausdorff space, the Stone space of either one of these algebras is the absolute of
is a compact Hausdorff space, the Stone space of either one of these algebras is the absolute of 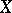 .
.
Canonical set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Canonical_set&oldid=46197