CW-complex

cellular decomposition

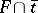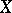A cell complex satisfying the following conditions: (C) for any the complex is finite, that is, consists of a finite number of cells. (For any subset of a cell complex , is the notation for the intersection of all subcomplexes of containing .) (W) If is some subset of and if for any cell in the intersection is closed in (and therefore in as well), then is a closed subset of . 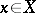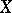In this connection, each point belongs to a definite set of , and .

The notation CW comes from the initial letters of the (English) names for the above two conditions — (C) for closure finiteness and (W) for weak topology.

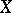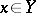A finite cell complex satisfies both conditions (C) and (W). More generally, a cell complex each point of which is contained in some finite subcomplex is a CW-complex. Let be a subset of such that is closed in for each cell in . Then for any the intersection is closed in . If the point does not belong to , then the open set contains and does not intersect 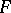. The set is open and is closed.

The class of CW-complexes (or the class of spaces of the same homotopy type as a CW-complex) is the most suitable class of topological spaces in relation to homotopy theory. Thus, if a subset of a CW-complex 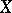is closed, then a mapping from the topological space into a topological space 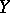is continuous if and only if the restrictions of to the closures of the cells of are continuous. If is a compact subset of a CW-complex , then the complex is finite. There exists for every cell 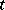of a CW-complex a set that is open in and has 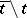as a deformation retract.

In practice, CW-complexes are constructed by an inductive procedure: Each stage consists in glueing cells of given dimension to the result of the previous stage. The cellular structure of such a complex is directly related to its homotopy properties. Even for such "good" spaces as polyhedra it is helpful to consider their representation as CW-complexes: There are usually fewer in such a representation than in a simplicial triangulation. If is obtained by attaching -dimensional cells to the space , then the subset , where , is a strong deformation retract of .

A relative CW-complex is a pair consisting of a topological space and a closed subset , together with a sequence of closed subspaces , , satisfying the following conditions: a) the space is obtained from by adjoining -cells; b) for , 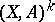is obtained from by adjoining -dimensional cells; c) ; d) the topology of is compatible with the family 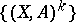. The space is called the 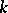-dimensional skeleton of relative to . When , the relative CW-complex is a CW-complex in the previous sense and its 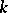-dimensional skeleton is .

Examples. 1) The pair 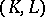of simplicial complexes 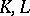, with , defines a relative CW-complex , where . 2) The ball 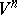is a CW-complex: 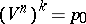for , and for . The sphere 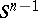is a subcomplex of the CW-complex 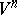. 3) If the pair is a relative CW-complex, then so is , and (when , is, by definition, ). 4) If 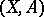is a relative CW-complex, then is a CW-complex and , where is the quotient space of obtained by identifying all points of with a single point.

References

[1]	C. Teleman, "Grundzüge der Topologie und differenzierbare Mannigfaltigkeiten" , Deutsch. Verlag Wissenschaft. (1968) (Translated from Rumanian)
[2]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)
[3]	A. Dold, "Lectures on algebraic topology" , Springer (1980)

Comments

CW-complexes have been introduced by J.H.C. Whitehead [a4] as a generalization of simplicial complexes (cf. Simplicial complex). An obvious advantage is that the number of cells needed in a decomposition is usually much smaller than the number of simplices in a triangulation. This is particularly profitable when computing homology and cohomology, and fundamental groups (cf. Fundamental group; [a1]). CW-complexes have proved useful in the context of classifying spaces for homotopy functors, and occur as Eilenberg–MacLane spaces (cf. Eilenberg–MacLane space).

Two textbooks specialized on CW-complexes are [a2] and [a3].

References

[a1]	R. Brown, "Elements of modern topology" , McGraw-Hill (1968)
[a2]	G.E. Cooke, P.L. Finney, "Homology of cell complexes" , Princeton Univ. Press (1967)
[a3]	A.T. Lundell, S. Weingram, "The topology of CW-complexes" , v. Nostrand (1969)
[a4]	J.H.C. Whitehead, "Combinatorial homotopy I" Bull. Amer. Math. Soc. , 55 (1949) pp. 213–245