Branching process with diffusion

A model of a branching process in which the reproducing particles diffuse in some domain 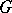. Let the domain 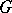be -dimensional, with an absorbing boundary 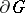, and let the particles in the domain itself execute mutually independent Brownian motions. Each particle in 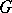is independently converted, within a time 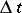, into particles with a probability of , , 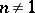. Let the daughter particles begin their independent evolution from the point of their genesis. Let

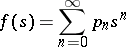be the generating function of 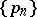, let 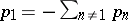, and let 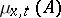be the number of particles in a set 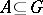at the moment 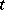if there initially was one particle at the point 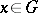. The generating functional

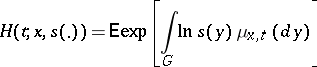satisfies the quasi-linear parabolic equation

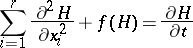with the initial condition

and the boundary condition

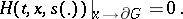Denote by 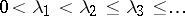the eigen values, and let 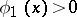be the eigen function of the problem

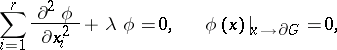corresponding to 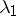. As 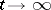the asymptotic relation

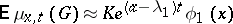holds. For this reason the problem is said to be subcritical if 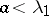, critical if 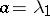and supercritical 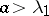if . If 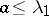, a branching process with diffusion dies out with probability one, while if 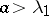, both the probability of dying out and the probability of the event 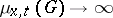as 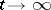will in general be positive. Depending on their criticality, branching processes with diffusion obey limit theorems analogous to those valid for branching processes without diffusion.

References

[1]	B.A. [B.A. Sevast'yanov] Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian)

Comments

Additional references can be found in the article Branching process.