Box spline
The box spline  associated with the
associated with the 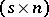 -matrix
-matrix 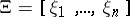 of its directions
of its directions 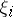 (assumed non-zero) is the distribution defined inductively by
(assumed non-zero) is the distribution defined inductively by
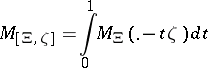 |
with  the point evaluation at
the point evaluation at 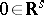 . This implies that
. This implies that  , with the integral taken over the half-open unit
, with the integral taken over the half-open unit  -cube
-cube 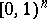 .
.
 is (representable as) a piecewise-polynomial function on the linear hull
is (representable as) a piecewise-polynomial function on the linear hull 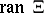 of its directions, with support in the convex hull of its directions, its polynomial degree being equal to
of its directions, with support in the convex hull of its directions, its polynomial degree being equal to 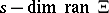 , its discontinuities on hyperplanes in
, its discontinuities on hyperplanes in 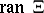 spanned by its directions, and its smoothness across such a hyperplane determined by the number of directions lying in that hyperplane.
spanned by its directions, and its smoothness across such a hyperplane determined by the number of directions lying in that hyperplane.
For 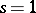 and
and 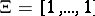 ,
, 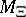 is the uniform or cardinal B-spline. Correspondingly, the extant box spline theory (see [a1]) is a partial lifting of Schoenberg's cardinal spline theory [a2]. Its highlights include a study of the linear independence of the integer translates of a box spline (with integer directions), the shift-invariant spaces spanned by the integer translates of one or more box splines, the dimension of the space of polynomials contained in such a box spline space, the refinability of such box splines and the related subdivision schemes and discrete box splines.
is the uniform or cardinal B-spline. Correspondingly, the extant box spline theory (see [a1]) is a partial lifting of Schoenberg's cardinal spline theory [a2]. Its highlights include a study of the linear independence of the integer translates of a box spline (with integer directions), the shift-invariant spaces spanned by the integer translates of one or more box splines, the dimension of the space of polynomials contained in such a box spline space, the refinability of such box splines and the related subdivision schemes and discrete box splines.
References
| [a1] | C. de Boor, K. Höllig, S. Riemenschneider, "Box splines" , Appl. Math. Sci. , 98 , Springer (1993) |
| [a2] | I.J. Schoenberg, "Cardinal spline interpolation" , CMBS , SIAM (1973) |
Box spline. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Box_spline&oldid=46141