Boundary value problem, ordinary differential equations
The problem of finding a solution to an equation
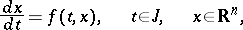 | (1) |
lying in a given subset  of the space
of the space 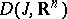 of functions depending on
of functions depending on 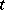 that are absolutely continuous on
that are absolutely continuous on 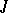 and that assume values in
and that assume values in 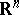 :
:
 | (2) |
It is assumed that 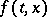 is a function defined on
is a function defined on  with values in
with values in 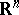 and satisfying the Carathéodory conditions;
and satisfying the Carathéodory conditions; 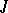 is an interval on the real line
is an interval on the real line 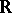 .
.
1) The boundary value problem (1), (2) is said to be linear if
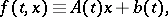 |
where the functions 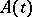 and
and  are summable on every compact interval in
are summable on every compact interval in 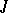 and the set
and the set 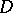 is a linear manifold in
is a linear manifold in 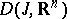 . In particular, one might have
. In particular, one might have
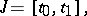 |
 |
where  is a function of bounded variation. A linear boundary value problem gives rise to a linear operator
is a function of bounded variation. A linear boundary value problem gives rise to a linear operator
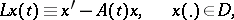 |
the eigen values of which are precisely those values of the parameter 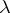 for which the homogeneous boundary value problem
for which the homogeneous boundary value problem
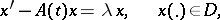 |
has non-trivial solutions. These non-trivial solutions are the eigen functions of the operator 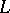 . If the inverse operator
. If the inverse operator  exists and has an integral representation
exists and has an integral representation
 |
then  is called a Green function.
is called a Green function.
2) Let  , let
, let  be almost-periodic in
be almost-periodic in 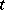 uniformly in
uniformly in  on every compact subset of
on every compact subset of 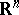 and let
and let 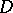 be the set of almost-periodic functions in
be the set of almost-periodic functions in 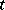 that are absolutely continuous on
that are absolutely continuous on 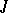 . Then problem (1), (2) is known as the problem of almost-periodic solutions.
. Then problem (1), (2) is known as the problem of almost-periodic solutions.
3) In control theory one considers boundary value problems with a functional parameter: a control. For example, consider the equation
 | (3) |
with set of admissible controls 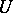 and two sets
and two sets 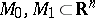 . Let
. Let 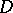 be the set of absolutely continuous functions in
be the set of absolutely continuous functions in 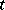 such that
such that  ,
, 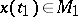 . The boundary value problem is to find a pair
. The boundary value problem is to find a pair 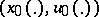 such that
such that 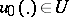 and the solution
and the solution  of equation (3) at
of equation (3) at 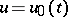 satisfies the condition
satisfies the condition  .
.
4) There is a wide range of diverse necessary and sufficient conditions for the existence and uniqueness of solutions to various boundary value problems, and of methods for constructing an approximate solution (see [4]–[7]). For example, consider the problem
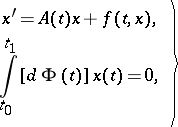 | (4) |
in which
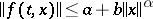 |
for certain constants 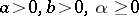 . Suppose that the homogeneous problem
. Suppose that the homogeneous problem
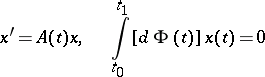 | (5) |
is regular, i.e. its only solution is the trivial one. Then problem (4) has at least one solution, provided either 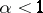 , or
, or 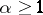 and
and 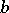 is sufficiently small. It is fairly complicated to determine whether problem (5) is regular. However, the linear (scalar) boundary value problem
is sufficiently small. It is fairly complicated to determine whether problem (5) is regular. However, the linear (scalar) boundary value problem
 |
for example, is regular if whenever 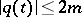 there exists a
there exists a  such that
such that
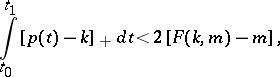 |
where
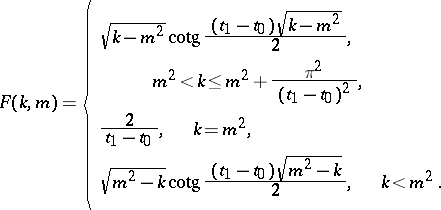 |
References
| [1] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [2] | M.A. Krasnosel'skii, V.Sh. Burd, Yu.S. Kolesov, "Nonlinear almost-periodic oscillations" , Wiley (1973) (Translated from Russian) |
| [3] | L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Interscience (1962) (Translated from Russian) |
| [4] | N.N. Krasovskii, "Theory of control of motion. Linear systems" , Moscow (1968) (In Russian) |
| [5] | V.I. Zubov, "Lectures in control theory" , Moscow (1975) (In Russian) |
| [6] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [7] | I.T. Kiguradze, "Some singular boundary value problems for ordinary differential equations" , Tbilisi (1975) (In Russian) |
Comments
References
| [a1] | M. Braun, "Differential equations and their applications" , Springer (1975) |
| [a2] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) pp. §§3.6, 3.51, 4.7, A.5 |
| [a3] | L.K. Jackson, "Boundary value problems for ordinary differential equations" J.K. Hale (ed.) , Studies in ordinary differential equations , Math. Assoc. Amer. (1977) pp. 93–127 |
Boundary value problem, ordinary differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_value_problem,_ordinary_differential_equations&oldid=46134