Borel summation method

A method for summing series of functions, proposed by E. Borel [1]. Suppose one is given a series of numbers

(*)

let 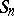be its partial sums and let 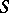be a real number. The series (*) is summable by the Borel method (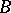-method) to the number 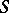if

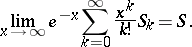There exists an integral summation method due to Borel. This is the 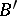-method: If

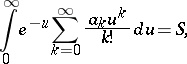then one says that the series (*) is summable by the 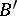-method to the number 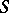. For conditions under which the two methods 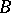and 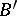are equivalent, cf. [2]. The -method originated in the context of analytic extension of a function regular at a point. Let

be regular at the point 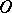and let 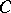be the set of all its singular points. Draw the segment and the straight line normal to through any point . The set of points on the same side with 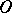for each straight line 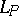is denoted by 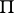; the boundary 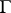of the domain 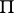is then called the Borel polygon of the function 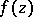, while the domain 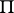is called its interior domain. The following theorem is valid: The series

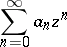is summable by the 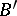-method in 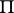, but not in the domain 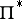which is the complement of 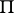[2].

References

[1]	E. Borel, "Mémoire sur les séries divergentes" Ann. Sci. École Norm. Sup. (3) , 16 (1899) pp. 9–131
[2]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)

References

[a1]	W. Beekmann, K. Zeller, "Theorie der Limitierungsverfahren" , Springer (1970)