Bieberbach polynomials

Extremal polynomials which approximate a function that conformally maps a given simply-connected domain onto a disc. These polynomials were first studied by L. Bieberbach [1] in the context of the problem of the approximate computation of a conformal mapping.

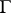Let be a simply-connected domain in the finite part of the plane bounded by a curve , and let the function 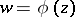map this domain conformally and univalently onto the disc 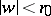under the conditions 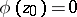and , where 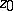is an arbitrary fixed point of and 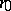depends on 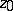. The polynomial 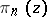which minimizes the integral

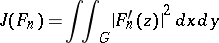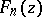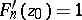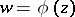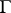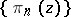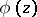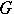in the class of all polynomials of degree subject to the conditions and is called the Bieberbach polynomial. In the class of all functions which are analytic in the domain and which satisfy the same conditions, this integral is minimized by the mapping function . If the contour is a Jordan curve, the sequence converges uniformly to the function inside . In the closed domain there need not be convergence [2]. If the contour 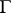satisfies certain additional smoothness conditions, the sequence 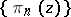converges uniformly in the closed domain, and the rate of convergence depends on the degree of smoothness of .

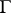References

[1]	L. Bieberbach, "Zur Theorie und Praxis der konformen Abbildung" Rend. Circ. Mat. Palermo , 38 (1914) pp. 98–112
[2]	M.V. Keldysh, "Sur l'approximation en moyenne quadratique des fonctions analytiques" Mat. Sb. , 5 (47) : 2 (1939) pp. 391–401
[3]	S.N. Mergelyan, "Some questions of the constructive theory of functions" Trudy Mat. Inst. Steklov. , 37 , Moscow (1951) (In Russian)
[4]	P.K. Suetin, "Polynomials orthogonal over a region and Bieberbach polynomials" Proc. Steklov Inst. Math. , 100 (1974) Trudy Mat. Inst. Steklov. , 100 (1971)

Comments

A good additional reference is [a1].

References

[a1]	D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980)