Berwald connection

Let denote the tangent bundle of a smooth -dimensional manifold , with zero-section removed. In Finsler geometry, one starts with a smooth metric function and its associated metric tensor, given locally by

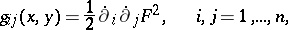where are the coordinates (positions and velocities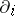) and and denote partial differentials with respect to and , respectively. It is assumed that is non-singular on and that and extend continuously to the entire tangent bundle 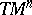. The pair 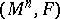is called a Finsler space. The Euler–Lagrange equations (cf. Euler–Lagrange equation) of 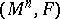describe geodesics (cf. Geodesic line) and have the local description

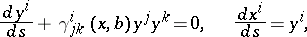where the differential of arc length is and 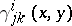are the usual Levi-Cività (or Christoffel) symbols (cf. Christoffel symbol) in terms of , its inverse and 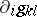. Note that the depend on 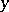. This is not the case in Riemannian geometry, where they are the coefficients of a unique, metric compatible, symmetric connection. In Finsler geometry there are several important connections, but 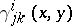itself is not a connection. One way to proceed is as follows. Let 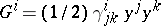and form 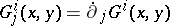and 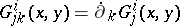. It can be readily proved that the 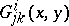transform like a classical affine connection, in spite of their dependence on 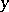, i.e.

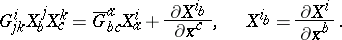Also, the have a transformation law induced from that of , because 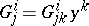, by the Euler theorem on homogeneous functions. Note that 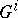, 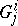and 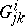are positively homogeneous in 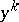of degree two, one and zero, respectively. The triple 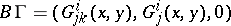is an example of a pre-Finsler connection [a1], 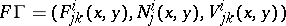, meaning that:

1) the 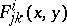transform just like the 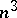functions 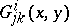above (they are called the coefficients of the pre-Finsler connection on );

2) the 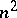functions 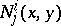transform just like 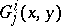(they are called the coefficients of a non-linear connection on ) and

3) 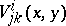is a tensor (cf. Tensor calculus) on .

Using these local expressions one can further introduce the vertical covariant derivative and the horizontal covariant derivative 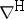, as follows: for any contravariant vector 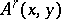, set

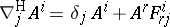1) and

2) , where is the Finsler delta-derivative operator on 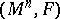corresponding to the non-linear connection 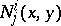. The important thing is that for any function 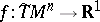, is a covariant vector. Similar rules for higher-order tensors 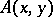are just what one expects and all of the above have global descriptions.

The Okada theorem states that for a pre–Finsler connecti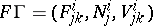on on 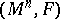such that:

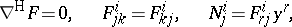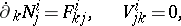one has . The pre-Finsler connection is the so-called Berwald connection on .

Curvature of the Berwald connection.

If is a contravariant vector, then

where 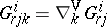defines the so-called (HV)-curvature, also known as the spray curvature or Douglas tensor [a1], [a2], [a3]) of 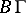. Also,

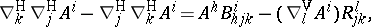where the Berwald curvature tensor is

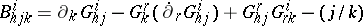and the VH-torsion tensor of 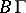is

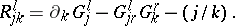Here, the symbol 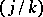denotes that the entire expression before it is to be rewritten with the indices 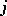and interchanged.

A fundamental result in Berwald geometry is that both 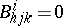and 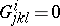if and only if 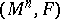is locally Minkowski. (Being locally Minkowski means that there is an admissible change of coordinates 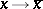so that 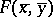is actually independent of .) Consequently, the geodesics in such a space have the local expression , .

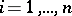Now, generally, in Berwald theory one has

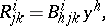whereas for ,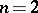

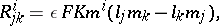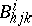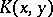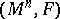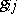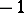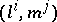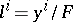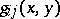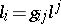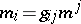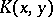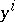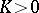so that is completely determined by the so-called Berwald–Gauss curvature of . The number equals if is positive definite and otherwise. The pair of contravariant vectors , where , is called the Berwald frame. The are normal vectors and are oriented. They are both of unit length and orthogonal relative to . Of course, and . The scalar invariant is positively homogeneous of degree zero in . If everywhere, then the geodesics of 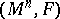are Lyapunov stable (cf. Lyapunov stability); if 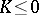everywhere, they are unstable [a1], [a4].

See also Berwald space.

References

[a1]	P.L. Antonelli, R.S. Ingarden, M. Matsumoto, "The theory of sprays and Finsler spaces with applications in physics and biology" , Kluwer Acad. Publ. (1993)
[a2]	P.L. Antonelli, T. (eds.) Zastawniak, "Lagrange geometry, Finsler spaces and noise applied in biology and physics" Math. and Comput. Mod. (Special Issue) , 20 (1994)
[a3]	M. Matsumoto, "Foundations of Finsler geometry and special Finsler spaces" , Kaiseisha Press (1986)
[a4]	H. Rund, "The differential geometry of Finsler spaces" , Springer (1959)