Bers space
A complex Banach space of holomorphic automorphic forms introduced by L. Bers (1961). Let  be an open set of the Riemann sphere
be an open set of the Riemann sphere  whose boundary consists of more than two points. Then
whose boundary consists of more than two points. Then  carries a unique complete conformal metric
carries a unique complete conformal metric  on
on  with curvature
with curvature  , known as the hyperbolic metric on
, known as the hyperbolic metric on  . Let
. Let  be a properly discontinuous group of conformal mappings of
be a properly discontinuous group of conformal mappings of  onto itself (cf. also Kleinian group; Conformal mapping). Typical examples of
onto itself (cf. also Kleinian group; Conformal mapping). Typical examples of  are Kleinian groups (cf. also Kleinian group), that is, a group of Möbius transformations (cf. also Fractional-linear mapping) of
are Kleinian groups (cf. also Kleinian group), that is, a group of Möbius transformations (cf. also Fractional-linear mapping) of 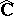 acting properly discontinuously on an open set of
acting properly discontinuously on an open set of  . By the conformal invariance, the hyperbolic area measure
. By the conformal invariance, the hyperbolic area measure  (
(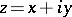 ) on
) on 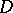 is projected to an area measure
is projected to an area measure  on the orbit space
on the orbit space  . In other words, let
. In other words, let  ,
, 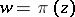 , where
, where  is the natural projection.
is the natural projection.
Fix an integer  . A holomorphic function
. A holomorphic function  on
on 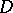 is called an automorphic form of weight
is called an automorphic form of weight 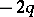 for
for 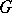 if
if  for all
for all  . Then
. Then  is invariant under the action of
is invariant under the action of  and hence may be considered as a function on
and hence may be considered as a function on  . The Bers space
. The Bers space  , where
, where  , is the complex Banach space of holomorphic automorphic forms
, is the complex Banach space of holomorphic automorphic forms  of weight
of weight  on
on 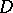 for
for  such that the function
such that the function  on
on  belongs to the space
belongs to the space  with respect to the measure
with respect to the measure  . The norm in
. The norm in  is thus given by
is thus given by
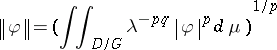 |
if 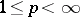 , and
, and
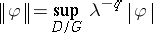 |
if  . Automorphic forms in
. Automorphic forms in  are said to be
are said to be 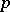 -integrable if
-integrable if  , and bounded if
, and bounded if  . When
. When 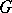 is trivial,
is trivial,  is abbreviated to
is abbreviated to  . Note that
. Note that  is isometrically embedded as a subspace of
is isometrically embedded as a subspace of  .
.
Some properties of Bers spaces.
1) Let 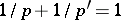 . The Petersson scalar product of
. The Petersson scalar product of  and
and  is defined by
is defined by
 |
If  , then the Petersson scalar product establishes an anti-linear isomorphism of
, then the Petersson scalar product establishes an anti-linear isomorphism of  onto the dual space of
onto the dual space of  , whose operator norm is between
, whose operator norm is between  and
and  .
.
2) The Poincaré (theta-) series of a holomorphic function  on
on  is defined by
is defined by
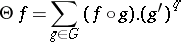 |
whenever the right-hand side converges absolutely and uniformly on compact subsets of  (cf. Absolutely convergent series; Uniform convergence). Then
(cf. Absolutely convergent series; Uniform convergence). Then  is an automorphic form of weight
is an automorphic form of weight  on
on  for
for  . Moreover,
. Moreover,  gives a continuous linear mapping of
gives a continuous linear mapping of  onto
onto  of norm at most
of norm at most  . For every
. For every  there exists an
there exists an  with
with  such that
such that  .
.
3) Let 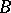 be the set of branch points of the natural projection
be the set of branch points of the natural projection 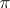 . Assume that: i)
. Assume that: i)  is obtained from a (connected) closed Riemann surface of genus
is obtained from a (connected) closed Riemann surface of genus 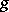 by deleting precisely
by deleting precisely  points; and ii)
points; and ii)  consists of exactly
consists of exactly  points
points  (possibly,
(possibly,  or
or  ). For each
). For each 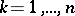 , let
, let  be the common multiplicity of
be the common multiplicity of  at points of
at points of  . Then
. Then 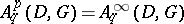 for
for 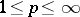 and
and
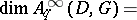 |
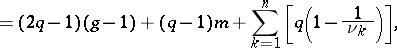 |
where 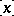 denotes the largest integer that does not exceed
denotes the largest integer that does not exceed  .
.
4) Consider the particular case where  is the unit disc. Then
is the unit disc. Then  is a Fuchsian group and
is a Fuchsian group and  . It had been conjectured that
. It had been conjectured that  for any
for any  , until Ch. Pommerenke [a6] constructed a counterexample. In [a5] D. Niebur and M. Sheingorn characterized the Fuchsian groups
, until Ch. Pommerenke [a6] constructed a counterexample. In [a5] D. Niebur and M. Sheingorn characterized the Fuchsian groups  for which the inclusion relation holds. In particular, if
for which the inclusion relation holds. In particular, if  is finitely generated, then
is finitely generated, then  .
.
5) Let  be a Fuchsian group acting on the unit disc
be a Fuchsian group acting on the unit disc  . It also preserves
. It also preserves  , the outside of the unit circle. If
, the outside of the unit circle. If  is conformal on
is conformal on  and can be extended to a quasi-conformal mapping of
and can be extended to a quasi-conformal mapping of 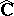 onto itself such that
onto itself such that  is a Möbius transformation for each
is a Möbius transformation for each  , then its Schwarzian derivative
, then its Schwarzian derivative
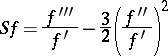 |
belongs to  with
with  . Moreover, the set of all such Schwarzian derivatives constitutes a bounded domain in
. Moreover, the set of all such Schwarzian derivatives constitutes a bounded domain in  including the open ball of radius
including the open ball of radius  centred at the origin. This domain can be regarded as a realization of the Teichmüller space
centred at the origin. This domain can be regarded as a realization of the Teichmüller space  of
of 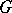 , and the injection of
, and the injection of  into
into 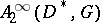 induced by the Schwarzian derivative is referred to as the Bers embedding.
induced by the Schwarzian derivative is referred to as the Bers embedding.
References
| [a1] | I. Kra, "Automorphic forms and Kleinian groups" , Benjamin (1972) |
| [a2] | J. Lehner, "Discontinuous groups and automorphic functions" , Amer. Math. Soc. (1964) |
| [a3] | J. Lehner, "Automorphic forms" W.J. Harvey (ed.) , Discrete Groups and Automorphic Functions , Acad. Press (1977) pp. 73–120 |
| [a4] | S. Nag, "The complex analytic theory of Teichmüller spaces" , Wiley (1988) |
| [a5] | D. Niebur, M. Sheingorn, "Characterization of Fuchsian groups whose integrable forms are bounded" Ann. of Math. , 106 (1977) pp. 239–258 |
| [a6] | Ch. Pommerenke, "On inclusion relations for spaces of automorphic forms" W.E. Kirwan (ed.) L. Zalcman (ed.) , Advances in Complex Function Theory , Lecture Notes in Mathematics , 505 , Springer (1976) pp. 92–100 |
Bers space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bers_space&oldid=46029