Bendixson sphere

The sphere in real analysis which is known as the Riemann sphere in the theory of functions of a complex variable.

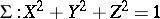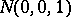Let be the unit sphere in the Euclidean -space, and let and be its north and south pole, respectively; let and 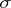be planes tangent to 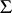at the points 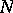and 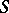respectively; let 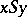and be coordinate systems in 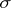and with axes parallel to the corresponding axes of the system in the plane 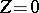and pointing in the same directions; let 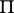be the stereographic projection of 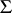onto 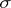from the centre 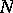, and let 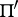be the stereographic projection of 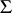onto from the centre 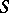. Then 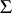is the Bendixson sphere with respect to any one of the planes 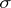, . It generates the bijection 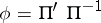of the plane 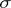(punctured at the point 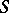) onto the plane , which is punctured at the point 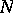. This bijection is employed in the study of the behaviour of the trajectories of an autonomous system of real algebraic ordinary differential equations of the second order in a neighbourhood of infinity in the phase plane (the right-hand sides of the equations are polynomials of the unknown functions). This bijection reduces the problem to a similar problem in a neighbourhood of the point 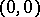. Named after I. Bendixson.

References

[1]	A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian)