Bateman method

A method for approximating the integral operator of a one-dimensional integral Fredholm equation of the second kind; it is a particular case of the method of degenerate kernels (cf. Degenerate kernels, method of). In Bateman's method, the degenerate kernel 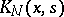is constructed according to the rule:

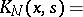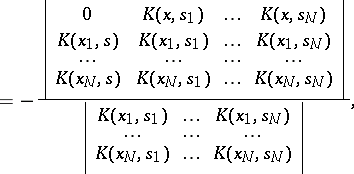where , are certain points on the integration segment of the integral equation considered. The method was proposed by H. Bateman [1].

References

[1]	H. Bateman, Messeng. Math. , 37 (1908) pp. 179–187
[2]	L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian)

References

[a1]	H. Bateman, Proc. Roy. Soc. A (1922) pp. 441–449