Bateman function
From Encyclopedia of Mathematics
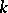 -function
-function
The function
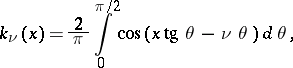 | (1) |
where  and
and  are real numbers. The function was defined by H. Bateman [1]. The Bateman function may be expressed in the form of a confluent hypergeometric function of the second kind
are real numbers. The function was defined by H. Bateman [1]. The Bateman function may be expressed in the form of a confluent hypergeometric function of the second kind 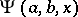 :
:
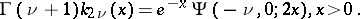 | (2) |
The relation (2) is conveniently taken as the definition of the Bateman function in the complex plane with the cut 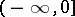 . The following relations are valid: for case (1)
. The following relations are valid: for case (1)
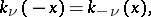 |
for case (2)
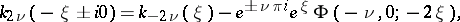 |
where 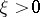 , and
, and 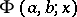 is a confluent hypergeometric function of the first kind.
is a confluent hypergeometric function of the first kind.
References
| [1] | H. Bateman, "The 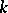 -function, a particular case of the confluent hypergeometric function" Trans. Amer. Math. Soc. , 33 (1931) pp. 817–831 -function, a particular case of the confluent hypergeometric function" Trans. Amer. Math. Soc. , 33 (1931) pp. 817–831 |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
How to Cite This Entry:
Bateman function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bateman_function&oldid=45995
Bateman function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bateman_function&oldid=45995
This article was adapted from an original article by L.N. Karmazina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article