Asymptotic power series

An asymptotic series with respect to the sequence

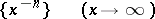or with respect to a sequence

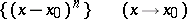(cf. Asymptotic expansion of a function). Asymptotic power series may be added, multiplied, divided and integrated just like convergent power series.

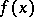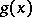Let two functions and have the following asymptotic expansions as :

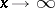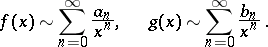Then

1)

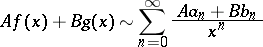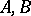( are constants);

2)

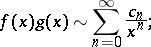3)

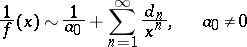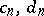( are calculated as for convergent power series);

4) if the function 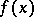is continuous for 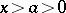, then

5) an asymptotic power series cannot always be differentiated, but if 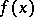has a continuous derivative which can be expanded into an asymptotic power series, then

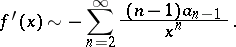Examples of asymptotic power series.

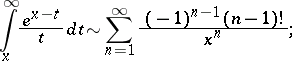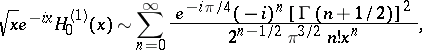where 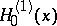is the Hankel function of order zero (cf. Hankel functions) (the above asymptotic power series diverge for all ).

Similar assertions are also valid for functions of a complex variable as 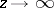in a neighbourhood of the point at infinity or inside an angle. For a complex variable 5) takes the following form: If the function 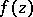is regular in the domain 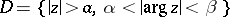and if

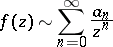uniformly in as inside any closed angle contained in 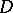, then

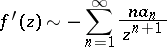uniformly in as 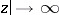in any closed angle contained in D.

References

[1]	E.T. Copson, "Asymptotic expansions" , Cambridge Univ. Press (1965)
[2]	A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956)
[3]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952)

References

[a1]	N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981)