Asymptotically-stable solution
A solution of a differential system that is stable according to Lyapunov (cf. Lyapunov stability) and that attracts all the other solutions with sufficiently close initial values. Thus, the solution
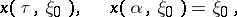 |
of the system
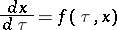 | (*) |
with a right-hand side 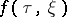 , given for all
, given for all  ,
, 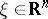 , and which is such that solutions of (*) exist and are unique, will be an asymptotically-stable solution if, together with all its sufficiently close solutions
, and which is such that solutions of (*) exist and are unique, will be an asymptotically-stable solution if, together with all its sufficiently close solutions
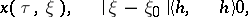 |
it is defined for all 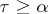 and if for an arbitrary
and if for an arbitrary 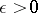 there exists a
there exists a 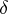 ,
, 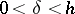 , such that
, such that 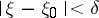 implies
implies
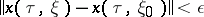 |
for all 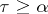 and
and
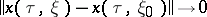 |
as 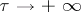 .
.
The concept of an asymptotically-stable solution was introduced by A.M. Lyapunov [1]; it, together with various special types of uniform asymptotic stability, is extensively used in the theory of stability [2], [3], [4].
References
| [1] | A.M. Lyapunov, "Problème général de la stabilité du mouvement" , Ann. of Math. Studies , 17 , Princeton Univ. Press (1947) |
| [2] | N.N. Krasovskii, "Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay" , Stanford Univ. Press (1963) (Translated from Russian) |
| [3] | W. Hahn, "Theorie und Anwendung der direkten Methode von Ljapunov" , Springer (1959) |
| [4] | N. Rouche, P. Habets, M. Laloy, "Stability theory by Liapunov's direct method" , Springer (1977) |
Comments
References
| [a1] | W. Hahn, "Stability of motion" , Springer (1967) pp. 422 |
Asymptotically-stable solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotically-stable_solution&oldid=45235