Associated function
From Encyclopedia of Mathematics
of a complex variable
A function which is obtained in some manner from a given function 
with the aid of some fixed function 
. For example, if
 |
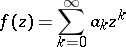is an entire function and if
 |
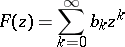is a fixed entire function with 
, 
, then
 |
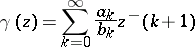is a function which is associated to 
by means of the function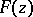 
; it is assumed that the series converges in some neighbourhood 
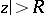. The function 
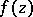is then represented in terms of 
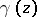by the formula
 |
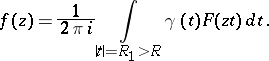In particular, if
 |
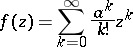is an entire function of exponential type and 
, then
 |
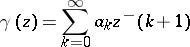is the Borel-associated function of 
(cf. Borel transform).
How to Cite This Entry:
Associated function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Associated_function&oldid=45229
Associated function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Associated_function&oldid=45229
This article was adapted from an original article by A.F. Leont'ev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article