Archimedean class
A class resulting from the subdivision induced by the Archimedean equivalence relation on a totally ordered semi-group. This equivalence is defined as follows. Two elements 
and 
of a semi-group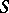 
are called Archimedean equivalent if one of the following four relations is satisfied:
 |
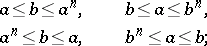which amounts to saying that 
and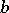 
generate the same convex sub-semi-group in 
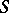. Thus, the subdivision into Archimedean classes is a subdivision into pairwise non-intersecting convex sub-semi-groups. Moreover, each subdivision into pairwise non-intersecting convex sub-semi-groups, can be extended to a subdivision into Archimedean classes.
The Archimedean equivalence on a totally ordered group is induced by the Archimedean equivalence of its positive cone: It is considered that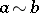 
if there exist positive integers 
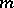and 
such that
 |
where
 |
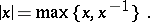The positive cone of an Archimedean group consists of a single Archimedean class.
Archimedean class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Archimedean_class&oldid=45211