Analytic mapping
analytic morphism
A morphism of analytic spaces considered as ringed spaces (cf. Analytic space; Ringed space). An analytic mapping of a space ( ) into a space (
) into a space ( ) is a pair
) is a pair 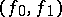 , where
, where
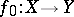 |
is a continuous mapping, while
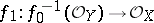 |
is a homomorphism of sheaves of rings on  . If the spaces are complex, an analytic mapping is also called a holomorphic mapping.
. If the spaces are complex, an analytic mapping is also called a holomorphic mapping.
If  and
and  are reduced analytic spaces, the homomorphism
are reduced analytic spaces, the homomorphism 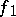 is completely determined by the mapping
is completely determined by the mapping 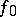 and is the inverse mapping of the germs of functions corresponding to
and is the inverse mapping of the germs of functions corresponding to 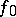 . Thus, in this case an analytic mapping is a mapping
. Thus, in this case an analytic mapping is a mapping 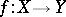 such that for any
such that for any 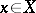 and for any
and for any 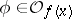 one has
one has 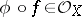 .
.
A fibre of an analytic mapping
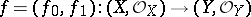 |
at a point  is the analytic subspace
is the analytic subspace
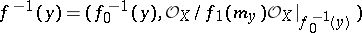 |
of the space 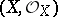 , where
, where 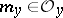 is the sheaf of germs of functions that vanish at the point
is the sheaf of germs of functions that vanish at the point 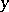 . Putting
. Putting
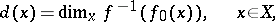 |
one obtains the inequality
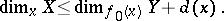 | (*) |
If 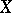 and
and 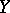 are reduced complex spaces, then the set
are reduced complex spaces, then the set
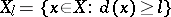 |
is analytic in 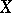 for any
for any 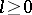 .
.
An analytic mapping 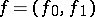 is called flat at a point
is called flat at a point 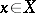 if
if  is a flat module over the ring
is a flat module over the ring 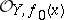 . In such a case (*) becomes an equality. An analytic mapping is called flat if it is flat at all points
. In such a case (*) becomes an equality. An analytic mapping is called flat if it is flat at all points 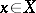 . A flat analytic mapping of complex spaces is open. Conversely, if
. A flat analytic mapping of complex spaces is open. Conversely, if 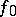 is open,
is open, 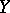 is smooth and all fibres are reduced, then
is smooth and all fibres are reduced, then 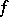 is a flat analytic mapping. The set of points of a complex or a rigid analytic space
is a flat analytic mapping. The set of points of a complex or a rigid analytic space 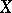 at which an analytic mapping
at which an analytic mapping 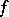 is not flat is analytic in
is not flat is analytic in 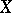 . If
. If 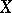 and
and  are reduced complex spaces, while
are reduced complex spaces, while 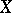 has a countable base, then
has a countable base, then 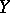 contains a dense everywhere-open set over which
contains a dense everywhere-open set over which  is a flat analytic mapping. If an analytic mapping
is a flat analytic mapping. If an analytic mapping
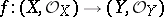 |
of complex spaces is flat, then the set of  at which the fibre
at which the fibre 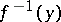 is not reduced or normal is analytic in
is not reduced or normal is analytic in 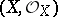 .
.
Let 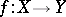 be an analytic mapping of reduced complex spaces. If
be an analytic mapping of reduced complex spaces. If 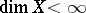 , then there exists a stratification
, then there exists a stratification
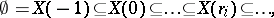 |
where 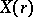 are analytic sets and
are analytic sets and  for large
for large  , with the following property: Any point
, with the following property: Any point 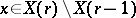 has a neighbourhood
has a neighbourhood 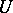 in
in 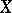 such that
such that 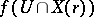 is a local analytic set in
is a local analytic set in 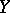 , all irreducible components of germs of which have dimension
, all irreducible components of germs of which have dimension  at
at  . If
. If 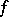 is proper, then
is proper, then 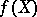 is an analytic set in
is an analytic set in 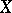 . This is a particular case of the finiteness theorem for analytic mappings.
. This is a particular case of the finiteness theorem for analytic mappings.
Let 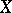 ,
, 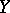 be complex spaces and let
be complex spaces and let  be compact. Then it is possible to endow the set
be compact. Then it is possible to endow the set 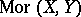 of all analytic mappings
of all analytic mappings  with the structure of a complex space such that the mapping
with the structure of a complex space such that the mapping
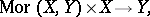 |
which maps the pair 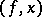 into
into 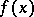 , is analytic. In particular, the group of automorphisms of a compact complex space
, is analytic. In particular, the group of automorphisms of a compact complex space 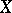 is a complex Lie group, acting analytically on
is a complex Lie group, acting analytically on 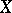 .
.
References
| [1] | R. Remmert, "Projektionen analytischer Mengen" Math. Ann. , 130 (1956) pp. 410–441 |
| [2] | R. Remmert, "Holomorphe und meromorphe Abbildungen komplexer Räume" Math. Ann. , 133 (1957) pp. 328–370 |
| [3] | K. Stein, , Colloquium for topology , Strasbourg (1954) |
| [4] | J. Frisch, "Points de plattitude d'une morphisme d'espaces analytiques complexes" Invent. Math. , 4 (1967) pp. 118–138 |
| [5] | G. Fisher, "Complex analytic geometry" , Springer (1976) |
Analytic mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_mapping&oldid=45176