Analytic function, element of an
The collection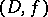 
of domains 
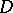in the plane 
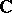of a complex variable 
and analytic functions 
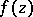given on 
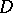by a certain analytic apparatus that allows one to effectively realize the analytic continuation of 
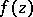to its whole domain of existence as a complete analytic function. The simplest and most frequently used form of an element of an analytic function is the circular element in the form of a power series
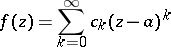 | (1) |
and its disc of convergence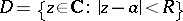 
with centre at 
(the centre of the element) and radius of convergence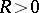 
. The analytic continuation here is achieved by a (possibly repeated) re-expansion of the series (1) for various centres 
, 
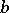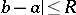, by formulas like
 |
 |
 |
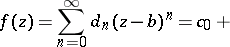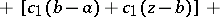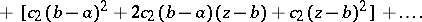Any one of the elements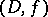 
of a complete analytic function determines it uniquely and can be represented by means of circular elements with centres 
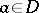. In the case of the centre at infinity, 
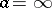, the circular element takes the form
 |
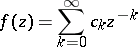with domain of convergence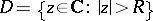 
.
In the process of the analytic continuation,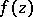 
may turn out to be multiple-valued and there may appear corresponding algebraic branch points (cf. Algebraic branch point), that is, branched elements of the form
 |
 |
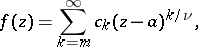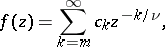where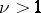 
; the number 
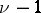is called the branching order. The branched elements generalize the concept of an element of an analytic function, which in this connection is also called an unramified (for 
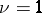) regular (for 
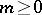) element.
As the simplest element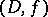 
of an analytic function 
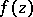of several complex variables 
, 
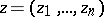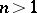, one can take a multiple power series
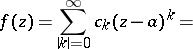 | (2) |
 |
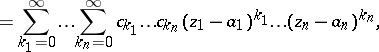where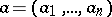 
is the centre, 
, 
, 
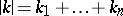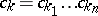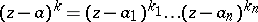, and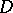 
is some polydisc
 |
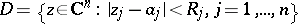in which the series (2) converges absolutely. However, for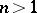 
one has to bear in mind that a polydisc is not the exact domain of absolute convergence of a power series.
The concept of an element of an analytic function is close to that of the germ of an analytic function.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
For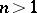 
the domain of absolute convergence of a power series is a so-called Reinhardt domain, cf. [a1].
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
Analytic function, element of an. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_function,_element_of_an&oldid=45168