Almost-reducible linear system
From Encyclopedia of Mathematics
of ordinary differential equations
A system
 | (*) |
 |
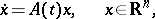having the following property: There exist a system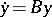 
, 
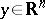, with constant coefficients and, for every 
, a Lyapunov transformation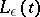 
such that by the change of variables 
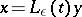, the system (*) is transformed into the system
 |
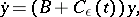where
 |
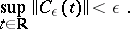Every reducible linear system is almost reducible.
References
| [1] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
How to Cite This Entry:
Almost-reducible linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-reducible_linear_system&oldid=45086
Almost-reducible linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-reducible_linear_system&oldid=45086
This article was adapted from an original article by V.M. Millionshchikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article