Affine pseudo-distance
From Encyclopedia of Mathematics
The number 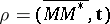 , equal to the modulus of the vector product of the vectors
, equal to the modulus of the vector product of the vectors  and
and 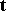 , where
, where 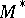 is an arbitrary point in an equi-affine plane,
is an arbitrary point in an equi-affine plane, 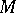 is a point on a plane curve
is a point on a plane curve 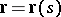 ,
,  is the affine parameter of the curve and
is the affine parameter of the curve and 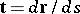 is the tangent vector at the point
is the tangent vector at the point  . This number
. This number 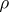 is called the affine pseudo-distance from
is called the affine pseudo-distance from  to
to 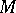 . If
. If  is held fixed, while
is held fixed, while  is moved along the curve, the affine pseudo-distance from
is moved along the curve, the affine pseudo-distance from  to
to  will assume a stationary value if and only if
will assume a stationary value if and only if  lies on the affine normal of the curve at
lies on the affine normal of the curve at 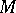 . An affine pseudo-distance in an equi-affine space can be defined in a similar manner for a given hypersurface.
. An affine pseudo-distance in an equi-affine space can be defined in a similar manner for a given hypersurface.
How to Cite This Entry:
Affine pseudo-distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_pseudo-distance&oldid=45048
Affine pseudo-distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_pseudo-distance&oldid=45048
This article was adapted from an original article by A.P. Shirokov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article