Additive selection
A mapping 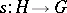 associated with a set-valued function
associated with a set-valued function 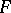 from an (Abelian) semi-group
from an (Abelian) semi-group 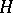 to subsets of an (Abelian) semi-group
to subsets of an (Abelian) semi-group 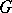 which is a homomorphism (of semi-groups) and a selection of
which is a homomorphism (of semi-groups) and a selection of 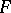 . If
. If 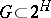 and
and 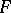 is the identity transformation on
is the identity transformation on 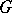 , then
, then  is said to be an additive selection on
is said to be an additive selection on 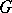 . An archetypical example of an additive selection is the mapping which subordinates to each non-empty compact set in
. An archetypical example of an additive selection is the mapping which subordinates to each non-empty compact set in  its maximal element. In
its maximal element. In 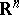 , similar selections can be defined by means of lexicographic orders, see [a1] and Lexicographic order). They are Borel measurable but not continuous with respect to the Hausdorff metric (for
, similar selections can be defined by means of lexicographic orders, see [a1] and Lexicographic order). They are Borel measurable but not continuous with respect to the Hausdorff metric (for 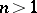 ). A Lipschitz-continuous additive selection on the family of convex bodies in
). A Lipschitz-continuous additive selection on the family of convex bodies in 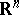 is given by associating with each convex body its Steiner point, see [a2]. No such selections can exist in infinite dimensions, see [a3], [a4].
is given by associating with each convex body its Steiner point, see [a2]. No such selections can exist in infinite dimensions, see [a3], [a4].
References
| [a1] | R. Živaljević, "Extremal Minkowski additive selections of compact convex sets" Proc. Amer. Math. Soc. , 105 (1989) pp. 697–700 |
| [a2] | R. Schneider, "Convex bodies: the Brunn–Minkowski theory" , Cambridge Univ. Press (1993) |
| [a3] | R.A. Vitale, "The Steiner point in infinite dimensions" Israel J. Math. , 52 (1985) pp. 245–250 |
| [a4] | K. Przesławski, D. Yost, "Continuity properties of selectors and Michael's theorem" Michigan Math. J. , 36 (1989) pp. 113–134 |
Additive selection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Additive_selection&oldid=45029