Absolute moment
of a random variable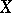 
The mathematical expectation of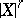 
, 
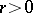. It is usually denoted by 
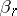, so that
 |
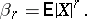The number 
is called the order of the absolute moment. If 
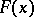is the distribution function of 
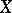, then
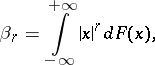 | (1) |
and, for example, if the distribution of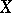 
has density 
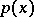, one has
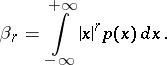 | (2) |
In relation to the equations (1) and (2) one also speaks, respectively, of the absolute moments of the distribution function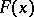 
and the density 
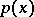. The existence of 
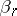implies the existence of the absolute moment 
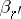and also of the moments (cf. Moment) of order 
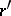, for 
. Absolute moments often appear in estimates of probability distributions and their characteristic functions (cf. Chebyshev inequality in probability theory; Lyapunov theorem). The function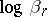 
is a convex function of 
, and the function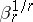 
is a non-decreasing function of 
, 
.
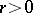Absolute moment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolute_moment&oldid=45005