Additive divisor problem
The problem of finding asymptotic values for sums of the form:
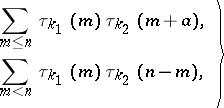 | (1) |
where 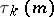 is the number of different factorizations of an integer
is the number of different factorizations of an integer 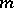 in
in 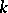 factors, counted according to multiplicity. Here
factors, counted according to multiplicity. Here 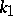 and
and 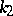 are integers
are integers 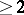 ,
,  is a fixed integer different from zero and
is a fixed integer different from zero and  is a sufficiently large number. In particular
is a sufficiently large number. In particular 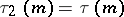 is the number of divisors of the number
is the number of divisors of the number 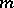 . Sums of the form (1) express the number of solutions of the equations
. Sums of the form (1) express the number of solutions of the equations
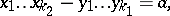 | (2) |
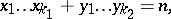 | (3) |
respectively. Particular cases of the additive divisor problem (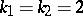 ,
,  and
and  ) are considered in [1]–[3]. The additive divisor problem with
) are considered in [1]–[3]. The additive divisor problem with  and an arbitrary positive integer
and an arbitrary positive integer 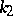 was solved using the dispersion method of Yu.V. Linnik [4].
was solved using the dispersion method of Yu.V. Linnik [4].
References
| [1] | A.E. Ingham, "Some asymptotic formulae in the theory of numbers" J. London Math. Soc. (1) , 2 (1927) pp. 202–208 |
| [2] | T. Esterman, "On the representations of a number as the sum of two products" Proc. London Math. Soc. (2) , 31 (1930) pp. 123–133 |
| [3] | C. Hooly, "An asymptotic formula in the theory of numbers" Proc. London Math. Soc. (3) , 7 (1957) pp. 396–413 |
| [4] | Yu.V. Linnik, "The dispersion method in binary additive problems" , Amer. Math. Soc. (1963) (Translated from Russian) |
Comments
The function 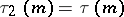 is also denoted by
is also denoted by 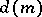 or
or 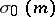 , cf. [a1], Sect. 16.7.
, cf. [a1], Sect. 16.7.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979) |
Additive divisor problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Additive_divisor_problem&oldid=44382