Bézier spline
A spline curve in 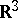 , where each polynomial spline segment is expressed in terms of Bernstein polynomials of a fixed degree. If the Bézier spline consists of only one segment, one speaks of a Bézier curve (cf. also Bézier curve). Bézier splines and curves are mainly used in the field of computer aided geometric design (CAGD), which is concerned with the design, approximation and representation of curves and surfaces by a computer. The Bézier representation overcomes numerical and geometric drawbacks of other polynomial forms. Bézier curves and surfaces were independently developed by P. de Casteljau at Citroën (about 1959) and by P. Bézier at Rénault (about 1962) for the construction of car bodies.
, where each polynomial spline segment is expressed in terms of Bernstein polynomials of a fixed degree. If the Bézier spline consists of only one segment, one speaks of a Bézier curve (cf. also Bézier curve). Bézier splines and curves are mainly used in the field of computer aided geometric design (CAGD), which is concerned with the design, approximation and representation of curves and surfaces by a computer. The Bézier representation overcomes numerical and geometric drawbacks of other polynomial forms. Bézier curves and surfaces were independently developed by P. de Casteljau at Citroën (about 1959) and by P. Bézier at Rénault (about 1962) for the construction of car bodies.
Given an interval 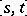 ,
, 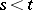 , the Bernstein polynomials over
, the Bernstein polynomials over 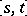 of degree
of degree  (cf. Bernstein polynomials) are defined by
(cf. Bernstein polynomials) are defined by
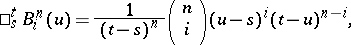 |
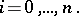 |
In many applications, 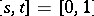 and then
and then 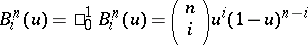 . Every polynomial of degree
. Every polynomial of degree  can be uniquely expressed in terms of
can be uniquely expressed in terms of 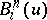 ,
, 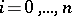 . Now, given
. Now, given 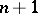 points
points 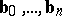 in
in 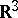 (or
(or 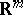 ,
, 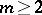 ), the polynomial parametric curve
), the polynomial parametric curve
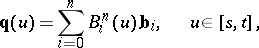 |
is said to be a Bézier curve of degree  over
over 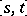 . The points
. The points 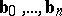 are called Bézier points of
are called Bézier points of 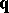 and they form the vertices of its so-called Bézier polygon. For every
and they form the vertices of its so-called Bézier polygon. For every 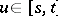 the point
the point 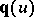 lies in the convex hull of
lies in the convex hull of 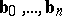 . Moreover,
. Moreover, 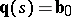 ,
, 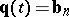 , and the lines
, and the lines 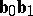 and
and 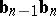 are tangent to
are tangent to  at
at  , respectively
, respectively  . The following de Casteljau algorithm is an efficient and stable method for evaluating
. The following de Casteljau algorithm is an efficient and stable method for evaluating 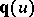 at
at 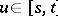 : Setting
: Setting 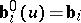 ,
, 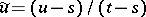 , and
, and
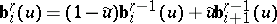 |
for 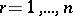 and
and 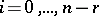 , one has
, one has  .
.
Now, let 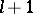 real values
real values  be given with
be given with  ,
, 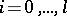 . Then a piecewise-polynomial continuous curve
. Then a piecewise-polynomial continuous curve 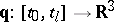 (or
(or 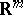 ,
, 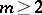 ) is called a Bézier spline of degree
) is called a Bézier spline of degree  if and only if each curve segment
if and only if each curve segment 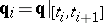 ,
, 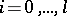 , is a Bézier curve of degree
, is a Bézier curve of degree  , that is, it has a representation
, that is, it has a representation
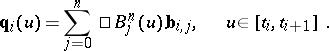 |
The  -continuity of
-continuity of  is equivalent to
is equivalent to  ,
,  . There are two concepts of continuity for the inner knots
. There are two concepts of continuity for the inner knots  . First, one can use the usual
. First, one can use the usual  -continuity of
-continuity of 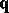 at the inner knots with respect to the given parameter
at the inner knots with respect to the given parameter  for each coordinate function of
for each coordinate function of 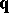 (cf. Spline).
(cf. Spline). 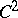 -continuous (Bézier) splines are sufficient for many practical applications.
-continuous (Bézier) splines are sufficient for many practical applications.
But, since a 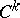 Bézier spline can have singularities, the weaker concept of geometric continuity was introduced. It is known that each rectifiable curve can be reparametrized so that the new parameter
Bézier spline can have singularities, the weaker concept of geometric continuity was introduced. It is known that each rectifiable curve can be reparametrized so that the new parameter  is arc length (see Natural parameter). A curve
is arc length (see Natural parameter). A curve 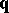 is called
is called 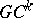 -continuous at a point
-continuous at a point 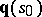 if and only if it is
if and only if it is 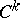 -continuous at this point with respect to arc length
-continuous at this point with respect to arc length  .
. 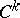 -continuity implies
-continuity implies 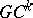 -continuity. A
-continuity. A 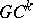 (Bézier) spline is
(Bézier) spline is 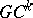 -continuous at its inner knots. For instance,
-continuous at its inner knots. For instance, 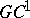 -continuity can be characterized by tangent continuity. Furthermore, a Bézier spline
-continuity can be characterized by tangent continuity. Furthermore, a Bézier spline 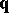 is
is 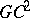 -continuous if and only if it has a continuous Frénet frame (cf. Frénet trihedron) and a continuous curvature at each inner knot. Explicit formulas for
-continuous if and only if it has a continuous Frénet frame (cf. Frénet trihedron) and a continuous curvature at each inner knot. Explicit formulas for 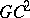 -continuity involving Bézier points can be found in the references below. Special representations of cubic
-continuity involving Bézier points can be found in the references below. Special representations of cubic 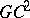 Bézier splines are cubic
Bézier splines are cubic  -splines and cubic
-splines and cubic  -splines (see [a3] or [a4]). For rational Bézier splines see the references below.
-splines (see [a3] or [a4]). For rational Bézier splines see the references below.
References
| [a1] | W. Boehm, G. Farin, J. Kahmann, "A survey of curve and surface methods in CAGD" Computer Aided Geometric Design , 1 (1984) pp. 1–60 |
| [a2] | J. Encarnaçao, W. Straßer, R. Klein, "Datenverarbeitung 1. Gerätetechnik, Programmierung und Anwendung graphischer Systeme" , R. Oldenbourg (1996) |
| [a3] | G. Farin, "Curves and surfaces for computer aided geometric design. A practical guide" , Acad. Press (1993) (Edition: Third) |
| [a4] | J. Hoschek, D. Lasser, "Grundlagen der geometrischen Datenverarbeitung" , Teubner (1992) (Edition: Second) |
| [a5] | M.E Mortensen, "Geometric modeling" , Wiley (1985) |
Bézier spline. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=B%C3%A9zier_spline&oldid=44369