Riemannian domain

Riemann domain, complex (-analytic) manifold over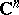

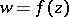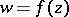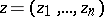An analogue of the Riemann surface of an analytic function of a single complex variable for the case of analytic functions , , of several complex variables , .

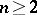More precisely, a path-connected Hausdorff space 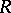is called an (abstract) Riemann domain if there is a local homeomorphism (a projection) 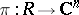such that for each point 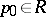there is a neighbourhood 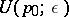that transforms homeomorphically into a polydisc

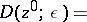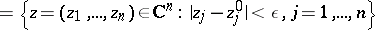in the complex space 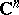. A Riemann domain is a separable space.

A complex function 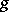is called holomorphic on 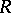if for any point 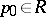the function 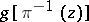of complex variables is holomorphic in the corresponding polydisc 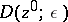. The projection 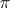is given by the choice of holomorphic functions 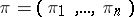, which correspond to coordinates in 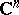. Starting from a given regular element of an analytic function 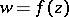, its Riemann domain is constructed in the same way as the Riemann surface of a given analytic function of one complex variable, i.e. initially by means of analytic continuation one constructs the complete analytic function 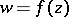, and then, using neighbourhoods, one introduces a topology into the set of elements of the complete analytic function. Like Riemann surfaces, Riemann domains arise unavoidably in connection with analytic continuation of a given element of an analytic function when, following the ideas of B. Riemann, one tries to represent the complete analytic function 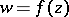as a single-valued point function on a domain.

In particular, Riemann domains arise as multi-sheeted domains of holomorphy of analytic functions of several complex variables. Oka's theorem states that a Riemann domain is a domain of holomorphy if and only if it is holomorphically convex (see Holomorphically-convex complex space).

Modern studies of Riemann domains are conducted within the framework of the general theory of analytic spaces. A generalization of the concept of a domain of holomorphy leads to Stein spaces (cf. Stein space).

References

[1]	B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian)
[2]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)
[3]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973)

Comments

The notion as presented above of a Riemann domain has been extended in several ways: Instead of 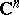one may choose any (model) complex-analytic space 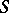(cf. Complex space). An unramified Riemann domain over 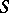is a tripl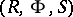e where 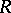is a complex-analytic space and 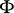is a locally biholomorphic mapping from 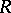into .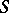

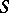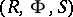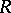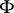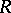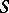Next, a ramified Riemann domain over is a triple where again is a complex-analytic space and is now a discrete open holomorphic mapping from to [a1].

References

[a1]	H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) pp. Chapt. VI (Elraged & Revised Edition. Original: 1934)
[a2]	H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German)