Diagonalizable algebraic group

An affine algebraic group 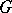that is isomorphic to a closed subgroup of an algebraic torus. Thus, 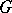is isomorphic to a closed subgroup of a multiplicative group of all diagonal matrices of given size. If 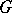is defined over a field 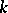and the isomorphism is defined over 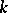, the diagonalizable algebraic group is said to be split (or decomposable) over .

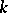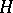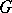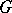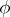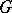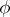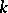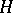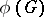Any closed subgroup in a diagonalizable algebraic group , as well as the image of under an arbitrary rational homomorphism , is a diagonalizable algebraic group. If, in addition, is defined and split over a field , while is defined over , then both and are defined and split over .

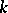A diagonalizable algebraic group is split over 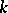if and only if elements in the group 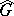of its rational characters are rational over 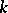. If 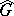contains no non-unit elements rational over 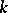, the diagonalizable algebraic group 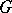is said to be anisotropic over 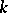. Any diagonalizable algebraic group 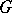defined over the field 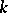is split over some finite separable extension of .

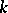A diagonalizable algebraic group is connected if and only if it is an algebraic torus. The connectedness of 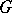is also equivalent to the absence of torsion in 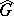. For any diagonalizable algebraic group defined over , the group 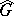is a finitely-generated Abelian group without 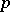-torsion, where 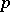is the characteristic of .

Any diagonalizable algebraic group 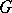which is defined and split over a field 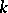is the direct product of a finite Abelian group and an algebraic torus defined and split over 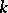. Any diagonalizable algebraic group 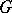which is connected and defined over a field 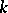contains a largest anisotropic subtorus 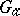and a largest subtorus 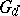which is split over 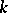; for these, 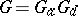, and 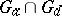is a finite set.

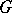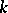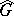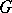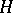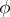If a diagonalizable algebraic group is defined over a field and is the Galois group of the separable closure of , then is endowed with a continuous action of . If, in addition, is a rational homomorphism between diagonalizable algebraic groups, while , and are defined over 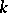, then the homomorphism 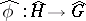is 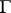-equivariant (i.e. is a homomorphism of 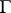-modules). The resulting contravariant functor from the category of diagonalizable 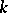-groups and their 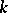-morphisms into the category of finitely-generated Abelian groups without 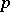-torsion with a continuous action of the group 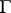and their 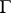-equivariant homomorphisms is an equivalence of these categories.

References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201
[2]	T. Ono, "Arithmetic of algebraic tori" Ann. of Math. , 74 : 1 (1961) pp. 101–139 MR0124326 Zbl 0119.27801

References

[a1]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039