User:Maximilian Janisch/latexlist/latex/12

List

1. 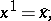 ; $x ^ { 1 } = \overline { x }$ ; confidence 0.575

2. 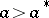 ; $\alpha > a ^ { * }$ ; confidence 0.575

3. 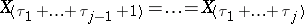 ; $X _ { ( \tau _ { 1 } + \ldots + \tau _ { j - 1 } + 1 ) } = \ldots = X _ { ( \tau _ { 1 } + \ldots + \tau _ { j } ) }$ ; confidence 0.575

4. 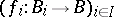 ; $( f _ { i } : B _ { i } \rightarrow B ) _ { i \in l }$ ; confidence 0.575

5. 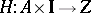 ; $H : A \times I \rightarrow Z$ ; confidence 0.575

6. 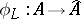 ; $\phi _ { L } : A \rightarrow A$ ; confidence 0.574

7. 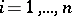 ; $i = 1 , \dots , n$ ; confidence 0.574

8. 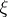 ; $5$ ; confidence 0.574

9. 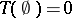 ; $T ( 0 ) = 0$ ; confidence 0.574

10. 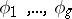 ; $\phi _ { 1 } , \ldots , \phi _ { g }$ ; confidence 0.573

11. 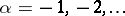 ; $\alpha = - 1 , - 2 , \ldots$ ; confidence 0.572

12. 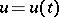 ; $u = u ( t )$ ; confidence 0.572

13. 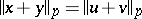 ; $\| x + y \| _ { p } = \| u + v \| _ { p }$ ; confidence 0.572

14. 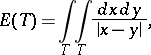 ; $E ( T ) = \int \int _ { T } \frac { d x d y } { | x - y | }$ ; confidence 0.572

15. 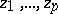 ; $z _ { 1 } , \ldots , z _ { p }$ ; confidence 0.572

16. 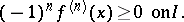 ; $( - 1 ) ^ { n } f ^ { ( n ) } ( x ) \geq 0 \text { on } I$ ; confidence 0.571

17.  ; $5$ ; confidence 0.571

18. 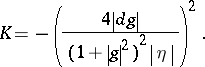 ; $K = - ( \frac { 4 | d g | } { ( 1 + | g | ^ { 2 } ) ^ { 2 } | \eta | } \} ^ { 2 }$ ; confidence 0.571

19.  ; $i$ ; confidence 0.570

20. 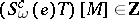 ; $( S _ { \omega } ^ { c } ( e ) T ) [ M ] \in Z$ ; confidence 0.570

21. 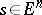 ; $s \in E ^ { n }$ ; confidence 0.570

22. 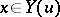 ; $x \in Y ( u )$ ; confidence 0.570

23. 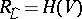 ; $R _ { L } = H ( V )$ ; confidence 0.569

24.  ; $f _ { B } ( x ) = \frac { \lambda ^ { x } } { x ! } e ^ { - \lambda } \{ 1 + \frac { \mu _ { 2 } - \lambda } { \lambda ^ { 2 } } [ \frac { x ^ { [ 2 ] } } { 2 } - \lambda x ^ { [ 1 ] } + \frac { \lambda ^ { 2 } } { 2 } ] +$ ; confidence 0.569

25. 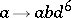 ; $a \rightarrow a b d ^ { 6 }$ ; confidence 0.569

26. 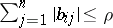 ; $\sum _ { j = 1 } ^ { n } | b _ { j j } | \leq \rho$ ; confidence 0.569

27. 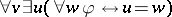 ; $\forall v \exists u ( \forall w \varphi \leftrightarrow u = w )$ ; confidence 0.569

28. 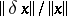 ; $\| \delta x \| f \| x \|$ ; confidence 0.569

29. 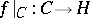 ; $f | c : C \rightarrow H$ ; confidence 0.568

30. 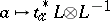 ; $\alpha \mapsto t _ { x } ^ { * } L \otimes L ^ { - 1 }$ ; confidence 0.568

31. 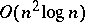 ; $O ( n ^ { 2 } \operatorname { log } n )$ ; confidence 0.568

32. 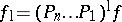 ; $f _ { 1 } = ( P _ { n } \ldots P _ { 1 } ) ^ { 1 } f$ ; confidence 0.568

33. 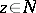 ; $z \in N$ ; confidence 0.568

34. 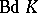 ; $B d K$ ; confidence 0.567

35. 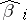 ; $\beta$ ; confidence 0.566

36.  ; $( X , B X )$ ; confidence 0.566

37. 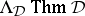 ; $\Lambda _ { D } \operatorname { Th } m D$ ; confidence 0.565

38. 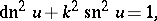 ; $dn ^ { 2 } u + k ^ { 2 } sn ^ { 2 } u = 1$ ; confidence 0.565

39. 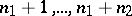 ; $n _ { 1 } + 1 , \ldots , n _ { 1 } + n _ { 2 }$ ; confidence 0.565

40. 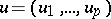 ; $u = ( u _ { 1 } , \ldots , u _ { p } )$ ; confidence 0.565

41. 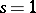 ; $s = 1$ ; confidence 0.564

42. 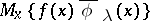 ; $\{ f ( x ) \overline { \phi } _ { \lambda } ( x ) \}$ ; confidence 0.564

43. 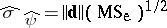 ; $\hat { \sigma } \hat { \psi } = \| d \| ( MS _ { e } ) ^ { 1 / 2 }$ ; confidence 0.563

44. 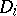 ; $D$ ; confidence 0.563

45. 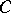 ; $C$ ; confidence 0.563

46. 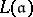 ; $L ( a )$ ; confidence 0.563

47. 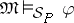 ; $\mathfrak { M } \vDash _ { S } _ { P } \varphi$ ; confidence 0.563

48. 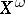 ; $X ^ { \omega }$ ; confidence 0.563

49. 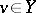 ; $v \in Y$ ; confidence 0.562

50. 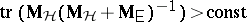 ; $\operatorname { tr } ( M _ { H } ( M _ { H } + M _ { E } ) ^ { - 1 } ) > c$ ; confidence 0.562

51.  ; $\geq 7$ ; confidence 0.562

52. 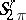 ; $S _ { 2 } ^ { \gamma }$ ; confidence 0.562

53. 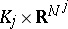 ; $K _ { j } \times R ^ { N j }$ ; confidence 0.562

54. 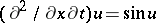 ; $( \partial ^ { 2 } / \partial x \partial t ) u = \operatorname { sin } u$ ; confidence 0.562

55. 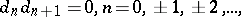 ; $d _ { n } d _ { n + 1 } = 0 , n = 0 , \pm 1 , \pm 2 , \dots$ ; confidence 0.562

56. 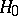 ; $H _ { 0 }$ ; confidence 0.561

57. 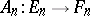 ; $A _ { n } : E _ { n } \rightarrow F _ { n }$ ; confidence 0.561

58. 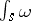 ; $\int _ { S } \omega$ ; confidence 0.561

59. 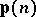 ; $p ( n )$ ; confidence 0.561

60. 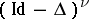 ; $( Id - \Delta ) ^ { \nu }$ ; confidence 0.560

61.  ; $E _ { \theta } \{ T \}$ ; confidence 0.560

62. 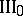 ; $III _ { 0 }$ ; confidence 0.560

63. 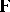 ; $1$ ; confidence 0.560

64.  ; $v$ ; confidence 0.560

65. 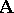 ; $\Delta$ ; confidence 0.559

66. 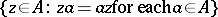 ; $\{ z \in A : z \alpha = \alpha z \text { for each } \alpha \in A \}$ ; confidence 0.559

67. 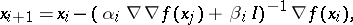 ; $x _ { i + 1 } = x _ { i } - ( \alpha _ { i } \nabla \nabla f ( x _ { j } ) + \beta _ { i } I ) ^ { - 1 } \nabla f ( x _ { i } )$ ; confidence 0.559

68. 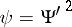 ; $\psi = \Psi ^ { \prime }$ ; confidence 0.559

69. 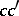 ; $e ^ { \prime }$ ; confidence 0.559

70. 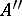 ; $A ^ { \prime \prime }$ ; confidence 0.559

71.  ; $k \geq n - i t$ ; confidence 0.558

72. 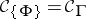 ; $c _ { \{ \Phi \} } = c _ { \Gamma }$ ; confidence 0.558

73. 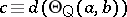 ; $c \equiv d ( \Theta _ { Q } ( a , b ) )$ ; confidence 0.557

74. 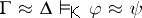 ; $\Gamma \approx \Delta \vDash _ { K } \varphi \approx \psi$ ; confidence 0.556

75. 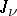 ; $J _ { \nu }$ ; confidence 0.556

76. 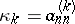 ; $\kappa _ { k } = a _ { n n } ^ { ( k ) }$ ; confidence 0.556

77. 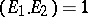 ; $( E _ { 1 } , E _ { 2 } ) = 1$ ; confidence 0.555

78. 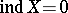 ; $X = 0$ ; confidence 0.554

79. 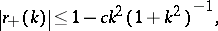 ; $| r _ { + } ( k ) | \leq 1 - c k ^ { 2 } ( 1 + k ^ { 2 } ) ^ { - 1 }$ ; confidence 0.554

80. 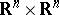 ; $R ^ { n } \times R ^ { n }$ ; confidence 0.554

81. 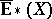 ; $\overline { E } * ( X )$ ; confidence 0.554

82. 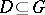 ; $D \subset G$ ; confidence 0.553

83. 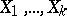 ; $X _ { 1 } , \ldots , X _ { k }$ ; confidence 0.553

84.  ; $x _ { n } \in D _ { A }$ ; confidence 0.553

85. 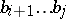 ; $b _ { i + 1 } \ldots b _ { j }$ ; confidence 0.553

86. 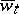 ; $\overline { w }$ ; confidence 0.553

87. 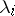 ; $\lambda _ { j }$ ; confidence 0.553

88. 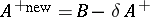 ; $A ^ { + \text { new } } = B - \delta A ^ { + }$ ; confidence 0.552

89. 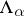 ; $\Lambda _ { a }$ ; confidence 0.552

90. 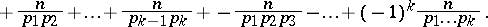 ; $+ \frac { n } { p _ { 1 } p _ { 2 } } + \ldots + \frac { n } { p _ { k - 1 } p _ { k } } + - \frac { n } { p _ { 1 } p _ { 2 } p _ { 3 } } - \ldots + ( - 1 ) ^ { k } \frac { n } { p _ { 1 } \ldots p _ { k } }$ ; confidence 0.552

91.  ; $( \frac { a - x } { z ^ { x } } + \ldots + \frac { a - 1 } { z } + f ( z ) ) d z$ ; confidence 0.552

92. 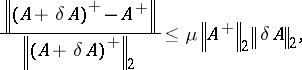 ; $\frac { \| ( A + \delta A ) ^ { + } - A ^ { + } \| } { \| ( A + \delta A ) ^ { + } \| _ { 2 } } \leq \mu \| A ^ { + } \| _ { 2 } \| \delta A _ { 2 }$ ; confidence 0.551

93. 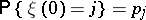 ; $P \{ \xi ( 0 ) = j \} = p _ { j }$ ; confidence 0.551

94. 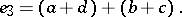 ; $e _ { 3 } = ( \alpha + d ) + ( b + c )$ ; confidence 0.551

95. 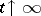 ; $t T \infty$ ; confidence 0.551

96. 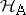 ; $H _ { A }$ ; confidence 0.550

97. 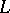 ; $L$ ; confidence 0.550

98. 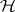 ; $74$ ; confidence 0.550

99. 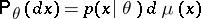 ; $P _ { \theta } ( d x ) = p ( x | \theta ) d \mu ( x )$ ; confidence 0.550

100. 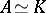 ; $A \simeq K$ ; confidence 0.550

101. 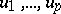 ; $u _ { 1 } , \dots , u _ { p }$ ; confidence 0.550

102. 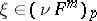 ; $\xi \in ( \nu F ^ { m } ) _ { p }$ ; confidence 0.549

103. 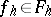 ; $f _ { h } \in F _ { k }$ ; confidence 0.549

104.  ; $c = E ( Y _ { 1 } )$ ; confidence 0.549

105. 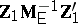 ; $Z _ { 1 } M _ { E } ^ { - 1 } Z _ { 1 } ^ { \prime }$ ; confidence 0.548

106. 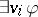 ; $\exists v ; \varphi$ ; confidence 0.548

107. 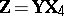 ; $Z = Y X$ ; confidence 0.548

108.  ; $S _ { 1 } = W _ { 1 }$ ; confidence 0.547

109. 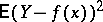 ; $E ( Y - f ( x ) ) ^ { 2 }$ ; confidence 0.547

110. 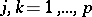 ; $j , k = 1 , \dots , p$ ; confidence 0.546

111. 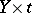 ; $Y \times t$ ; confidence 0.546

112. 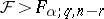 ; $F > F _ { \alpha ; q , n - \gamma }$ ; confidence 0.546

113. 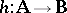 ; $h ; A \rightarrow B$ ; confidence 0.546

114. 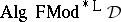 ; $D$ ; confidence 0.545

115. 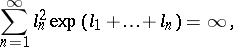 ; $\sum _ { n = 1 } ^ { \infty } l _ { k } ^ { 2 } \operatorname { exp } ( l _ { 1 } + \ldots + l _ { n } ) = \infty$ ; confidence 0.545

116. 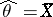 ; $\hat { \theta } = X$ ; confidence 0.545

117. 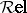 ; $R el$ ; confidence 0.544

118. 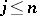 ; $j \leq n$ ; confidence 0.544

119. 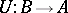 ; $U : B \rightarrow A$ ; confidence 0.544

120. 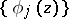 ; $\{ \phi j ( z ) \}$ ; confidence 0.543

121. 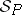 ; $S _ { P }$ ; confidence 0.543

122. 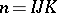 ; $n = I K$ ; confidence 0.542

123.  ; $x \in D _ { A }$ ; confidence 0.542

124. 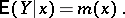 ; $E ( Y | x ) = m ( x )$ ; confidence 0.542

125. 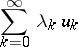 ; $\sum _ { k = 0 } ^ { \infty } \lambda _ { k } u _ { k }$ ; confidence 0.542

126. 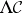 ; $\Delta C$ ; confidence 0.542

127. 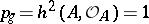 ; $p _ { g } = h ^ { 2 } ( A , O _ { A } ) = 1$ ; confidence 0.542

128. 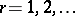 ; $r = 1,2 , \dots$ ; confidence 0.541

129. 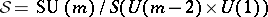 ; $S = SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$ ; confidence 0.541

130. 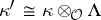 ; $\kappa ^ { \prime } \cong \kappa \otimes O \Lambda$ ; confidence 0.541

131. 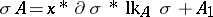 ; $\sigma A = x ^ { * } \partial \sigma ^ { * } \operatorname { lk } _ { A } \sigma + A _ { 1 }$ ; confidence 0.541

132. 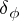 ; $\delta _ { \phi }$ ; confidence 0.541

133. 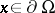 ; $x \in \partial \Omega$ ; confidence 0.540

134. 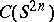 ; $C ( S ^ { 2 n } )$ ; confidence 0.540

135. 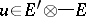 ; $u \in E ^ { \prime } \otimes - E$ ; confidence 0.540

136. 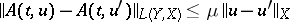 ; $\| A ( t , u ) - A ( t , u ^ { \prime } ) \| _ { L ( Y , X ) } \leq \mu \| u - u ^ { \prime } \| _ { X }$ ; confidence 0.540

137. 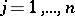 ; $j = 1 , \ldots , n$ ; confidence 0.539

138. 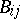 ; $B i$ ; confidence 0.539

139. 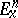 ; $E _ { X } ^ { N }$ ; confidence 0.539

140. 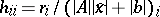 ; $h _ { i i } = r _ { i } / ( | A | | x | + | b | ) _ { i }$ ; confidence 0.539

141. 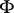 ; $\Phi$ ; confidence 0.539

142. 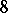 ; $D$ ; confidence 0.538

143. 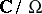 ; $C / \Omega$ ; confidence 0.538

144. 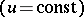 ; $( u = const )$ ; confidence 0.538

145. 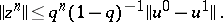 ; $\| z ^ { n } \| \leq q ^ { n } ( 1 - q ) ^ { - 1 } \| u ^ { 0 } - u ^ { 1 } \|$ ; confidence 0.538

146.  ; $\Omega ^ { * } S$ ; confidence 0.538

147. 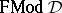 ; $D$ ; confidence 0.538

148. 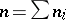 ; $n = \sum n$ ; confidence 0.537

149. 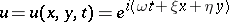 ; $u = u ( x , y , t ) = e ^ { i ( \omega t + \xi x + \eta y ) }$ ; confidence 0.537

150. 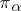 ; $\pi _ { 0 }$ ; confidence 0.537

151. 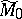 ; $\hat { M } _ { 0 }$ ; confidence 0.537

152. 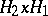 ; $H _ { 2 } \times H _ { 1 }$ ; confidence 0.537

153. 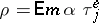 ; $\rho = E m \alpha \tau _ { j } ^ { e }$ ; confidence 0.537

154. 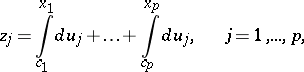 ; $z _ { j } = \int _ { c _ { 1 } } ^ { x _ { 1 } } d u _ { j } + \ldots + \int _ { c _ { p } } ^ { x _ { p } } d u _ { j } , \quad j = 1 , \ldots , p$ ; confidence 0.537

155. 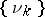 ; $\{ \nu _ { k } \}$ ; confidence 0.536

156.  ; $f \in C ^ { 1 } ( [ 0 , T ] ; X )$ ; confidence 0.535

157. 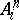 ; $A$ ; confidence 0.535

158. 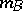 ; $m B$ ; confidence 0.535

159. 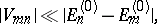 ; $| V _ { m n } | \ll | E _ { n } ^ { ( 0 ) } - E _ { m } ^ { ( 0 ) } |$ ; confidence 0.535

160. 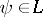 ; $\psi \in L$ ; confidence 0.533

161. 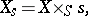 ; $X _ { s } = X \times s s$ ; confidence 0.533

162. 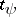 ; $t _ { \gamma }$ ; confidence 0.533

163. 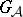 ; $G$ ; confidence 0.533

164. 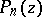 ; $P _ { N } ( z )$ ; confidence 0.533

165. 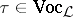 ; $\tau \in V o c$ ; confidence 0.532

166. 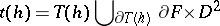 ; $t ( h ) = T ( h ) \cup \partial T ( k ) \partial F \times D ^ { 2 }$ ; confidence 0.532

167. 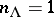 ; $n _ { \Delta } = 1$ ; confidence 0.532

168. 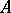 ; $4$ ; confidence 0.531

169. 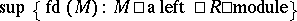 ; $\{ fd ( M )$ ; confidence 0.531

170. 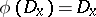 ; $\phi ( D _ { X } ) = D _ { X }$ ; confidence 0.531

171. 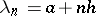 ; $\lambda _ { x } = a + n h$ ; confidence 0.530

172. 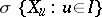 ; $\{ X _ { i } : u \in I \}$ ; confidence 0.529

173. 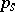 ; $P s$ ; confidence 0.529

174.  ; $\rho ( | A ^ { - 1 } \delta A | ) < 1$ ; confidence 0.528

175.  ; $\{ A _ { 1 } , \dots , A _ { l } \}$ ; confidence 0.527

176. 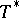 ; $T ^ { * }$ ; confidence 0.527

177. 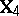 ; $x$ ; confidence 0.527

178. 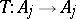 ; $T : A _ { j } \rightarrow A$ ; confidence 0.526

179.  ; $- i \partial / \partial x _ { j }$ ; confidence 0.526

180. 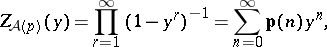 ; $Z _ { A ( p ) } ( y ) = \prod _ { r = 1 } ^ { \infty } ( 1 - y ^ { r } ) ^ { - 1 } = \sum _ { n = 0 } ^ { \infty } p ( n ) y ^ { n }$ ; confidence 0.525

181. 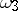 ; $w _ { 3 }$ ; confidence 0.525

182. 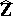 ; $z$ ; confidence 0.525

183.  ; $( 5 \times 10 ^ { 6 } r ) ^ { 3 }$ ; confidence 0.525

184. 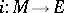 ; $\therefore M \rightarrow E$ ; confidence 0.524

185. 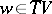 ; $w \in T V$ ; confidence 0.524

186. 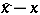 ; $\overline { X } - X$ ; confidence 0.524

187. 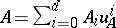 ; $A = \sum _ { i = 0 } ^ { d } A _ { i } u _ { A } ^ { i }$ ; confidence 0.523

188.  ; $P ( \mathfrak { m } / \mathfrak { m } ^ { 2 } )$ ; confidence 0.523

189. 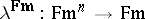 ; $\lambda ^ { Fm } : Fm ^ { n } \rightarrow Fm$ ; confidence 0.522

190. 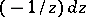 ; $( - 1 / z ) d z$ ; confidence 0.522

191. 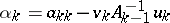 ; $\alpha _ { k } = a _ { k k } - v _ { k } A _ { k - 1 } ^ { - 1 } u _ { k }$ ; confidence 0.522

192. 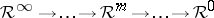 ; $R ^ { \infty } \rightarrow \ldots \rightarrow R ^ { m } \rightarrow \ldots \rightarrow R ^ { 0 }$ ; confidence 0.522

193. 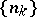 ; $\{ n _ { k } \}$ ; confidence 0.521

194. 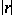 ; $| v |$ ; confidence 0.521

195. 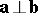 ; $a \perp b$ ; confidence 0.521

196. 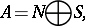 ; $A = N \oplus s$ ; confidence 0.521

197. 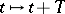 ; $t \mapsto t + T$ ; confidence 0.520

198. 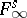 ; $F _ { \infty } ^ { s }$ ; confidence 0.520

199. 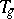 ; $T$ ; confidence 0.520

200. 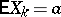 ; $E X _ { k } = a$ ; confidence 0.520

201. 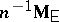 ; $n ^ { - 1 } M _ { E }$ ; confidence 0.519

202. 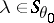 ; $\lambda \in S _ { \theta _ { 0 } }$ ; confidence 0.519

203. 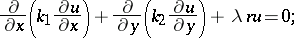 ; $\frac { \partial } { \partial x } ( k _ { 1 } \frac { \partial u } { \partial x } ) + \frac { \partial } { \partial y } ( k _ { 2 } \frac { \partial u } { \partial y } ) + \lambda n = 0$ ; confidence 0.519

204. 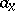 ; $a _ { y }$ ; confidence 0.519

205. 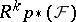 ; $R ^ { k } p \times ( F )$ ; confidence 0.519

206. 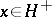 ; $x \in H ^ { + }$ ; confidence 0.518

207. 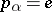 ; $p _ { \alpha } = e$ ; confidence 0.518

208. 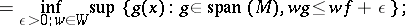 ; $\operatorname { inf } _ { \epsilon > 0 ; \mu \in W } \operatorname { sup } \{ g ( x ) : g \in \operatorname { span } ( M ) , w g \leq w f + \epsilon \}$ ; confidence 0.518

209. 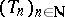 ; $( T _ { n } ) _ { n \in N }$ ; confidence 0.517

210. 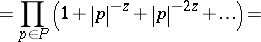 ; $= \prod _ { p \in P } ( 1 + | p | ^ { - z } + | p | ^ { - 2 z } + \ldots ) =$ ; confidence 0.517

211. 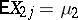 ; $E X _ { 2 j } = \mu _ { 2 }$ ; confidence 0.517

212. 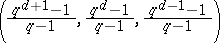 ; $( \frac { q ^ { d + 1 } - 1 } { q ^ { - 1 } } , \frac { q ^ { d } - 1 } { q ^ { - 1 } } , \frac { q ^ { d - 1 } - 1 } { q ^ { - 1 } } )$ ; confidence 0.517

213. 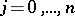 ; $j = 0 , \dots , n$ ; confidence 0.517

214. 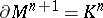 ; $\partial M ^ { n + 1 } = K ^ { n }$ ; confidence 0.516

215. 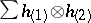 ; $\sum h _ { ( 1 ) } \otimes h _ { ( 2 ) }$ ; confidence 0.516

216.  ; $\phi = ( \phi _ { 1 } , \ldots , \phi _ { n } )$ ; confidence 0.516

217. 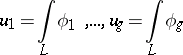 ; $u _ { 1 } = \int _ { L } \phi _ { 1 } , \ldots , u _ { g } = \int _ { L } \phi _ { g }$ ; confidence 0.516

218. 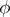 ; $( 1 )$ ; confidence 0.515

219. 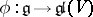 ; $\phi : \mathfrak { g } \rightarrow \mathfrak { g } ( V )$ ; confidence 0.515

220. 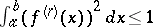 ; $\int _ { a } ^ { b } ( f ^ { ( r ) } ( x ) ) ^ { 2 } d x \leq 1$ ; confidence 0.515

221. 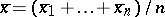 ; $x = ( x _ { 1 } + \ldots + x _ { n } ) / n$ ; confidence 0.514

222. 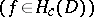 ; $( f \in H _ { C } ( D ) )$ ; confidence 0.513

223. 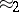 ; $\sim 2$ ; confidence 0.512

224. 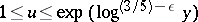 ; $1 \leq u \leq \operatorname { exp } ( \operatorname { log } ( 3 / 5 ) - \epsilon _ { y } )$ ; confidence 0.512

225. 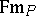 ; $Fm _ { F }$ ; confidence 0.512

226. 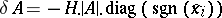 ; $\delta A = - H . | A | \cdot \operatorname { diag } ( \operatorname { sgn } ( x _ { i } ) )$ ; confidence 0.511

227.  ; $p _ { U } ( x ) \leq p _ { V K } ( x _ { 0 } ) + \epsilon$ ; confidence 0.511

228. 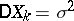 ; $DX _ { k } = \sigma ^ { 2 }$ ; confidence 0.511

229. 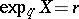 ; $\operatorname { exp } _ { q } X = r$ ; confidence 0.511

230. 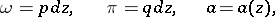 ; $\omega = p d z , \quad \pi = q d z , \quad \alpha = \alpha ( z )$ ; confidence 0.510

231.  ; $\mathfrak { g } = C$ ; confidence 0.510

232. 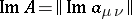 ; $\operatorname { lm } A = \| \operatorname { lm } \alpha _ { \mu \nu } |$ ; confidence 0.510

233. 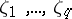 ; $\zeta _ { 1 } , \ldots , \zeta _ { q }$ ; confidence 0.510

234. 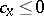 ; $c _ { X } \leq 0$ ; confidence 0.509

235. 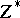 ; $Z ^ { * }$ ; confidence 0.508

236. 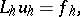 ; $L _ { h } u _ { k } = f _ { k }$ ; confidence 0.508

237. 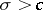 ; $\sigma > c$ ; confidence 0.508

238. 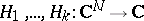 ; $H _ { 1 } , \ldots , H _ { k } : C ^ { M } \rightarrow C$ ; confidence 0.507

239. 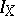 ; $I _ { X }$ ; confidence 0.507

240. 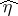 ; $\pi$ ; confidence 0.507

241.  ; $\Phi _ { t } = id$ ; confidence 0.507

242. 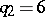 ; $q 2 = 6$ ; confidence 0.507

243. 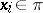 ; $x _ { i } \in \pi$ ; confidence 0.507

244. 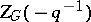 ; $Z _ { G } ( - q ^ { - 1 } )$ ; confidence 0.506

245. 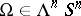 ; $\Omega \in \Delta ^ { n } S$ ; confidence 0.506

246. 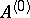 ; $A ^ { ( 0 ) }$ ; confidence 0.506

247. 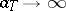 ; $a T \rightarrow \infty$ ; confidence 0.506

248. 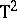 ; $T ^ { 2 }$ ; confidence 0.505

249. 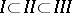 ; $I \subset I I \subset M$ ; confidence 0.505

250.  ; $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$ ; confidence 0.505

251.  ; $D : \mathfrak { D } \rightarrow A$ ; confidence 0.505

252. 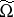 ; $\tilde { \Omega }$ ; confidence 0.505

253. 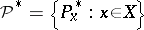 ; $P ^ { * } = \{ P _ { X } ^ { * } : x \in X \}$ ; confidence 0.505

254. 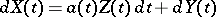 ; $d X ( t ) = a ( t ) Z ( t ) d t + d Y ( t )$ ; confidence 0.505

255. 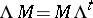 ; $M = M \Lambda ^ { t }$ ; confidence 0.505

256. 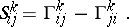 ; $S _ { j } ^ { k } = \Gamma _ { i j } ^ { k } - \Gamma _ { j i } ^ { k }$ ; confidence 0.505

257. 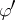 ; $\phi ^ { \prime }$ ; confidence 0.504

258. 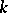 ; $k$ ; confidence 0.504

259. 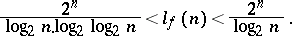 ; $\frac { 2 ^ { n } } { \operatorname { log } _ { 2 } n \cdot \operatorname { log } _ { 2 } \operatorname { log } _ { 2 } n } < l _ { f } ( n ) < \frac { 2 ^ { n } } { \operatorname { log } _ { 2 } n }$ ; confidence 0.504

260. 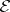 ; $\varepsilon$ ; confidence 0.504

261. 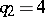 ; $q 2 = 4$ ; confidence 0.504

262. 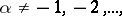 ; $\alpha \neq - 1 , - 2 , \dots ,$ ; confidence 0.504

263. 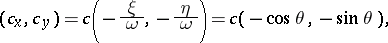 ; $( c _ { x } , c _ { y } ) = c ( - \frac { \xi } { \omega } , - \frac { \eta } { \omega } ) = c ( - \operatorname { cos } \theta , - \operatorname { sin } \theta )$ ; confidence 0.503

264. 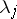 ; $\lambda$ ; confidence 0.503

265. 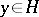 ; $y \in H$ ; confidence 0.503

266. 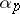 ; $\alpha p$ ; confidence 0.503

267. 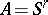 ; $A = S ^ { \prime }$ ; confidence 0.502

268. 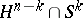 ; $H ^ { n - k } \cap S ^ { k }$ ; confidence 0.502

269. 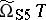 ; $\tilde { \Omega } _ { S 5 } T$ ; confidence 0.501

270. 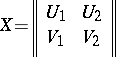 ; $X = \| \left. \begin{array} { l l } { U _ { 1 } } & { U _ { 2 } } \\ { V _ { 1 } } & { V _ { 2 } } \end{array} \right. |$ ; confidence 0.501

271. 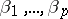 ; $\beta _ { 1 } , \ldots , \beta _ { p }$ ; confidence 0.501

272. 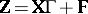 ; $Z = X \Gamma + F$ ; confidence 0.500

273.  ; $\Sigma ( M ) = B ^ { + } \cup _ { S ( M ) } B ^ { - }$ ; confidence 0.500

274. 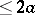 ; $< 2 a$ ; confidence 0.500

275.  ; $\ldots < t _ { - 1 } < t _ { 0 } \leq 0 < t _ { 1 } < t _ { 2 } <$ ; confidence 0.500

276. 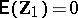 ; $E ( Z _ { 1 } ) = 0$ ; confidence 0.500

277. 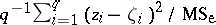 ; $q ^ { - 1 } \sum _ { i = 1 } ^ { q } ( z _ { i } - \zeta _ { i } ) ^ { 2 } / MS _ { e }$ ; confidence 0.500

278. 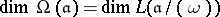 ; $\Omega ( a ) = \operatorname { dim } L ( a / ( \omega ) )$ ; confidence 0.499

279. 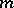 ; $m$ ; confidence 0.499

280. 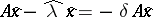 ; $A x - \hat { \lambda } x = - \delta A x$ ; confidence 0.499

281. 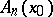 ; $A _ { n } ( x _ { 0 } )$ ; confidence 0.499

282. 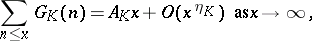 ; $\sum _ { n \leq x } G _ { K } ( n ) = A _ { K } x + O ( x ^ { \eta } K ) \text { as } x \rightarrow \infty$ ; confidence 0.498

283. 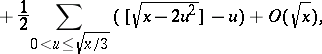 ; $+ \frac { 1 } { 2 } \sum _ { 0 < u \leq \sqrt { x / 3 } } ( [ \sqrt { x - 2 u ^ { 2 } } ] - u ) + O ( \sqrt { x } )$ ; confidence 0.498

284. 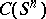 ; $C ( S ^ { n } )$ ; confidence 0.498

285. 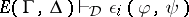 ; $E ( \Gamma , \Delta ) \dagger _ { D } \epsilon _ { i } ( \varphi , \psi )$ ; confidence 0.498

286. 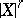 ; $| X | ^ { \prime }$ ; confidence 0.497

287. 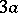 ; $3 a$ ; confidence 0.497

288. 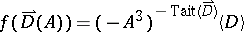 ; $f ( \vec { D } ( A ) ) = ( - A ^ { 3 } ) ^ { - \operatorname { Tait } ( \vec { D } ) } \langle D \rangle$ ; confidence 0.497

289. 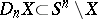 ; $D _ { n } X \subset S ^ { n } \backslash X$ ; confidence 0.497

290. 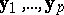 ; $y _ { 1 } , \dots , y _ { p }$ ; confidence 0.497

291. 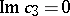 ; $\operatorname { lm } c _ { 3 } = 0$ ; confidence 0.496

292. 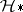 ; $74$ ; confidence 0.496

293. 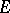 ; $k$ ; confidence 0.496

294. 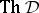 ; $\operatorname { Th } D$ ; confidence 0.496

295. 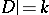 ; $D = k$ ; confidence 0.495

296. 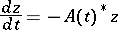 ; $\frac { d z } { d t } = - A ( t ) ^ { * } Z$ ; confidence 0.495

297. 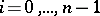 ; $i = 0 , \ldots , n - 1$ ; confidence 0.495

298. 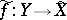 ; $\tilde { f } : Y \rightarrow X$ ; confidence 0.494

299.  ; $\pi _ { p } ( T ) = \operatorname { inf } c$ ; confidence 0.493

300. 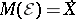 ; $M ( E ) = \vec { X }$ ; confidence 0.493