User:Maximilian Janisch/Sandbox

This page is a copy of the article Bayesian approach in order to test automatic LaTeXification. This article is not my work.

to statistical problems

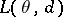An approach based on the assumption that to any parameter in a statistical problem there can be assigned a definite probability distribution. Any general statistical decision problem is determined by the following elements: by a space of (potential) samples , by a space of values of the unknown parameter , by a family of probability distributions on , by a space of decisions and by a function , which characterizes the losses caused by accepting the decision when the true value of the parameter is . The objective of decision making is to find in a certain sense an optimal rule (decision function) 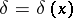, assigning to each result of an observation 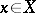the decision 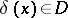. In the Bayesian approach, when it is assumed that the unknown parameter 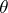is a random variable with a given (a priori) distributi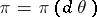on on 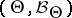the best decision function (Bayesian decision function) 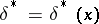is defined as the function for which the minimum expected loss 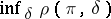, where

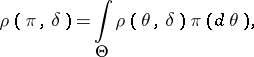and

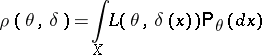is attained. Thus,

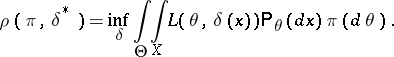In searching for the Bayesian decision function 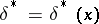, the following remark is useful. Let 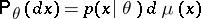, , 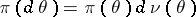where 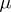and are certain 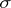-finite measures. One then finds, assuming that the order of integration may be changed,

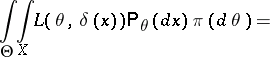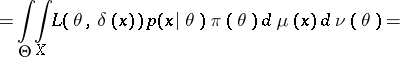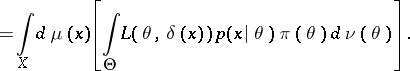It is seen from the above that for a given 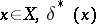is that value of 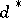for which

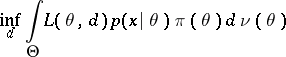is attained, or, what is equivalent, for which

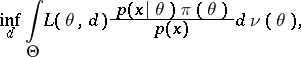is attained, where

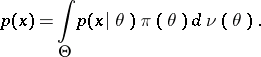But, according to the Bayes formula

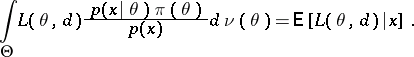Thus, for a given , 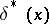is that value of for which the conditional average loss attains a minimum.

Example. (The Bayesian approach applied to the case of distinguishing between two simple hypotheses.) Let 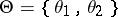, , 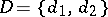, 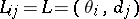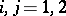; , , 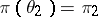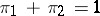. If the solution 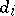is identified with the acceptance of the hypothesis 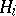: 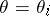, it is natural to assume that 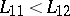, 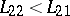. Then

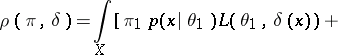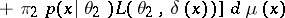implies that is attained for the function

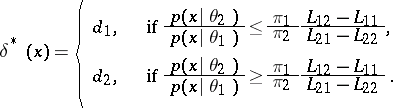The advantage of the Bayesian approach consists in the fact that, unlike the losses 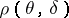, the expected losses are numbers which are dependent on the unknown parameter , and, consequently, it is known that solutions 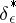for which

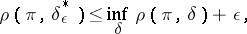and which are, if not optimal, at least -optimal 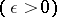, are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. Bayesian approach, empirical).

References

[1]	A. Wald, "Statistical decision functions" , Wiley (1950)
[2]	M.H. de Groot, "Optimal statistical decisions" , McGraw-Hill (1970)