User:Maximilian Janisch/latexlist/latex/11
List
1. 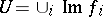 ; $$U = \cup _ { i } \operatorname { Im } f$$ ; confidence 0.671
; $$U = \cup _ { i } \operatorname { Im } f$$ ; confidence 0.671
2. 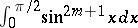 ; $$\int _ { 0 } ^ { \pi / 2 } \operatorname { sin } ^ { 2 m + 1 } x d x$$ ; confidence 0.964
; $$\int _ { 0 } ^ { \pi / 2 } \operatorname { sin } ^ { 2 m + 1 } x d x$$ ; confidence 0.964
3. 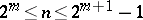 ; $$2 ^ { m } \leq n \leq 2 ^ { m + 1 } - 1$$ ; confidence 0.976
; $$2 ^ { m } \leq n \leq 2 ^ { m + 1 } - 1$$ ; confidence 0.976
4. 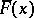 ; $$F ( x )$$ ; confidence 1.000
; $$F ( x )$$ ; confidence 1.000
5. 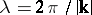 ; $$\lambda = 2 \pi / | k |$$ ; confidence 0.980
; $$\lambda = 2 \pi / | k |$$ ; confidence 0.980
6. 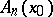 ; $$A _ { n } ( x _ { 0 } )$$ ; confidence 0.499
; $$A _ { n } ( x _ { 0 } )$$ ; confidence 0.499
7. 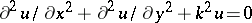 ; $$\partial ^ { 2 } u / \partial x ^ { 2 } + \partial ^ { 2 } u / \partial y ^ { 2 } + k ^ { 2 } u = 0$$ ; confidence 0.997
; $$\partial ^ { 2 } u / \partial x ^ { 2 } + \partial ^ { 2 } u / \partial y ^ { 2 } + k ^ { 2 } u = 0$$ ; confidence 0.997
8. 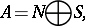 ; $$A = N \oplus s$$ ; confidence 0.521
; $$A = N \oplus s$$ ; confidence 0.521
9.  ; $$A = N \oplus S _ { 1 }$$ ; confidence 0.438
; $$A = N \oplus S _ { 1 }$$ ; confidence 0.438
10. 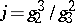 ; $$j = g ^ { 3 } / g ^ { 2 }$$ ; confidence 0.799
; $$j = g ^ { 3 } / g ^ { 2 }$$ ; confidence 0.799
11. 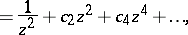 ; $$= \frac { 1 } { z ^ { 2 } } + c 2 z ^ { 2 } + c _ { 4 } z ^ { 4 } + \ldots$$ ; confidence 0.426
; $$= \frac { 1 } { z ^ { 2 } } + c 2 z ^ { 2 } + c _ { 4 } z ^ { 4 } + \ldots$$ ; confidence 0.426
12. 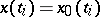 ; $$x ( t _ { i } ) = x _ { 0 } ( t _ { i } )$$ ; confidence 0.980
; $$x ( t _ { i } ) = x _ { 0 } ( t _ { i } )$$ ; confidence 0.980
13. 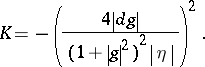 ; $$K = - ( \frac { 4 | d g | } { ( 1 + | g | ^ { 2 } ) ^ { 2 } | \eta | } \} ^ { 2 }$$ ; confidence 0.571
; $$K = - ( \frac { 4 | d g | } { ( 1 + | g | ^ { 2 } ) ^ { 2 } | \eta | } \} ^ { 2 }$$ ; confidence 0.571
14. 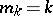 ; $$m _ { k } = \dot { k }$$ ; confidence 0.352
; $$m _ { k } = \dot { k }$$ ; confidence 0.352
15. 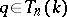 ; $$q \in T _ { n } ( k )$$ ; confidence 0.977
; $$q \in T _ { n } ( k )$$ ; confidence 0.977
16. 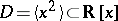 ; $$D = \langle x ^ { 2 } \} \subset R [ x ]$$ ; confidence 0.413
; $$D = \langle x ^ { 2 } \} \subset R [ x ]$$ ; confidence 0.413
17. 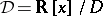 ; $$D = R [ x ] / D$$ ; confidence 0.968
; $$D = R [ x ] / D$$ ; confidence 0.968
18. 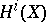 ; $$H ^ { i } ( X )$$ ; confidence 0.995
; $$H ^ { i } ( X )$$ ; confidence 0.995
19.  ; $$H ^ { 2 n } ( X )$$ ; confidence 0.999
; $$H ^ { 2 n } ( X )$$ ; confidence 0.999
20.  ; $$\beta$$ ; confidence 0.911
; $$\beta$$ ; confidence 0.911
21. 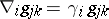 ; $$\nabla _ { i g j k } = \gamma _ { i } g _ { j k }$$ ; confidence 0.315
; $$\nabla _ { i g j k } = \gamma _ { i } g _ { j k }$$ ; confidence 0.315
22. 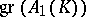 ; $$\operatorname { gr } ( A _ { 1 } ( K ) )$$ ; confidence 0.860
; $$\operatorname { gr } ( A _ { 1 } ( K ) )$$ ; confidence 0.860
23.  ; $$A _ { k + 1 } ( C )$$ ; confidence 0.634
; $$A _ { k + 1 } ( C )$$ ; confidence 0.634
24. 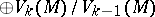 ; $$\oplus V _ { k } ( M ) / V _ { k - 1 } ( M )$$ ; confidence 0.970
; $$\oplus V _ { k } ( M ) / V _ { k - 1 } ( M )$$ ; confidence 0.970
25. 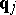 ; $$q$$ ; confidence 0.899
; $$q$$ ; confidence 0.899
26. 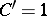 ; $$C ^ { \prime } = 1$$ ; confidence 0.999
; $$C ^ { \prime } = 1$$ ; confidence 0.999
27.  ; $$W ( f \times g ) = W ( f ) . W ( g )$$ ; confidence 0.906
; $$W ( f \times g ) = W ( f ) . W ( g )$$ ; confidence 0.906
28. 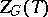 ; $$Z _ { \zeta } ( T )$$ ; confidence 0.463
; $$Z _ { \zeta } ( T )$$ ; confidence 0.463
29. 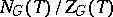 ; $$N _ { G } ( T ) / Z _ { G } ( T )$$ ; confidence 0.990
; $$N _ { G } ( T ) / Z _ { G } ( T )$$ ; confidence 0.990
30. 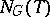 ; $$N _ { G } ( T )$$ ; confidence 0.970
; $$N _ { G } ( T )$$ ; confidence 0.970
31. 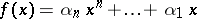 ; $$f ( x ) = \alpha _ { n } x ^ { n } + \ldots + \alpha _ { 1 } x$$ ; confidence 0.966
; $$f ( x ) = \alpha _ { n } x ^ { n } + \ldots + \alpha _ { 1 } x$$ ; confidence 0.966
32. 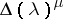 ; $$\Delta ( \lambda ) ^ { \mu }$$ ; confidence 1.000
; $$\Delta ( \lambda ) ^ { \mu }$$ ; confidence 1.000
33. 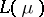 ; $$L ( \mu )$$ ; confidence 0.993
; $$L ( \mu )$$ ; confidence 0.993
34. 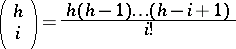 ; $$\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$$ ; confidence 0.487
; $$\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$$ ; confidence 0.487
35. 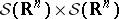 ; $$S ( R ^ { n } ) \times S ( R ^ { n } )$$ ; confidence 0.944
; $$S ( R ^ { n } ) \times S ( R ^ { n } )$$ ; confidence 0.944
36.  ; $$\alpha ^ { \psi } = Op ( J ^ { 1 / 2 } \alpha )$$ ; confidence 0.058
; $$\alpha ^ { \psi } = Op ( J ^ { 1 / 2 } \alpha )$$ ; confidence 0.058
37. 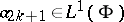 ; $$\alpha _ { 2 k + 1 } \in L ^ { 1 } ( \Phi )$$ ; confidence 0.712
; $$\alpha _ { 2 k + 1 } \in L ^ { 1 } ( \Phi )$$ ; confidence 0.712
38. 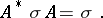 ; $$A ^ { * } \sigma A = \sigma$$ ; confidence 0.887
; $$A ^ { * } \sigma A = \sigma$$ ; confidence 0.887
39.  ; $$G = G ^ { \sigma }$$ ; confidence 0.956
; $$G = G ^ { \sigma }$$ ; confidence 0.956
40. 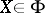 ; $$X \in \Phi$$ ; confidence 0.895
; $$X \in \Phi$$ ; confidence 0.895
41. 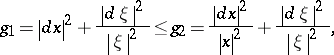 ; $$g _ { 1 } = | d x | ^ { 2 } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } } \leq g = \frac { | d x | ^ { 2 } } { | x | ^ { 2 } } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } }$$ ; confidence 0.357
; $$g _ { 1 } = | d x | ^ { 2 } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } } \leq g = \frac { | d x | ^ { 2 } } { | x | ^ { 2 } } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } }$$ ; confidence 0.357
42.  ; $$\pi _ { 4 n - 1 } ( S ^ { 2 n } ) \rightarrow \pi _ { 4 n } ( S ^ { 2 n + 1 } )$$ ; confidence 0.354
; $$\pi _ { 4 n - 1 } ( S ^ { 2 n } ) \rightarrow \pi _ { 4 n } ( S ^ { 2 n + 1 } )$$ ; confidence 0.354
43. 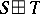 ; $$S \square T$$ ; confidence 0.898
; $$S \square T$$ ; confidence 0.898
44.  ; $$T _ { n }$$ ; confidence 0.602
; $$T _ { n }$$ ; confidence 0.602
45. 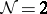 ; $$N = 2$$ ; confidence 0.996
; $$N = 2$$ ; confidence 0.996
46. 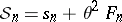 ; $$S _ { n } = s _ { n } + \theta ^ { 2 } F _ { n }$$ ; confidence 0.942
; $$S _ { n } = s _ { n } + \theta ^ { 2 } F _ { n }$$ ; confidence 0.942
47. 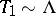 ; $$T _ { 1 } \sim \Lambda$$ ; confidence 0.998
; $$T _ { 1 } \sim \Lambda$$ ; confidence 0.998
48. 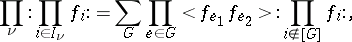 ; $$\prod _ { \nu } : \prod _ { i \in I _ { \nu } } f _ { i } : = \sum _ { G } \prod _ { e \in G } < f _ { e _ { 1 } } f _ { e _ { 2 } } > : \prod _ { i \notin [ G ] } f _ { i : }$$ ; confidence 0.238
; $$\prod _ { \nu } : \prod _ { i \in I _ { \nu } } f _ { i } : = \sum _ { G } \prod _ { e \in G } < f _ { e _ { 1 } } f _ { e _ { 2 } } > : \prod _ { i \notin [ G ] } f _ { i : }$$ ; confidence 0.238
49. 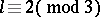 ; $$l \equiv 2 ( \operatorname { mod } 3 )$$ ; confidence 0.997
; $$l \equiv 2 ( \operatorname { mod } 3 )$$ ; confidence 0.997
50. 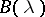 ; $$B ( \lambda )$$ ; confidence 1.000
; $$B ( \lambda )$$ ; confidence 1.000
51. 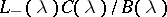 ; $$L _ { - } ( \lambda ) C ( \lambda ) / B ( \lambda )$$ ; confidence 0.885
; $$L _ { - } ( \lambda ) C ( \lambda ) / B ( \lambda )$$ ; confidence 0.885
52. 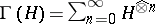 ; $$\Gamma ( H ) = \sum _ { n = 0 } ^ { \infty } H ^ { \otimes n }$$ ; confidence 0.591
; $$\Gamma ( H ) = \sum _ { n = 0 } ^ { \infty } H ^ { \otimes n }$$ ; confidence 0.591
53. 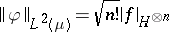 ; $$\| \varphi \| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } | f | _ { H ^ { \otimes n } }$$ ; confidence 0.909
; $$\| \varphi \| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } | f | _ { H ^ { \otimes n } }$$ ; confidence 0.909
54. 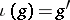 ; $$( g ) = g ^ { \prime }$$ ; confidence 1.000
; $$( g ) = g ^ { \prime }$$ ; confidence 1.000
55. 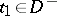 ; $$t _ { 1 } \in D ^ { - }$$ ; confidence 0.997
; $$t _ { 1 } \in D ^ { - }$$ ; confidence 0.997
56. 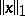 ; $$\| x \| _ { 1 }$$ ; confidence 0.650
; $$\| x \| _ { 1 }$$ ; confidence 0.650
57. 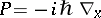 ; $$P = - i \hbar \nabla _ { x }$$ ; confidence 0.929
; $$P = - i \hbar \nabla _ { x }$$ ; confidence 0.929
58. 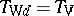 ; $$T _ { W \alpha } = T$$ ; confidence 0.134
; $$T _ { W \alpha } = T$$ ; confidence 0.134
59. 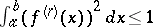 ; $$\int _ { a } ^ { b } ( f ^ { ( r ) } ( x ) ) ^ { 2 } d x \leq 1$$ ; confidence 0.515
; $$\int _ { a } ^ { b } ( f ^ { ( r ) } ( x ) ) ^ { 2 } d x \leq 1$$ ; confidence 0.515
60. 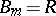 ; $$B _ { m } = R$$ ; confidence 0.993
; $$B _ { m } = R$$ ; confidence 0.993
61. 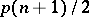 ; $$p ( n + 1 ) / 2$$ ; confidence 0.997
; $$p ( n + 1 ) / 2$$ ; confidence 0.997
62. 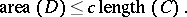 ; $$( D ) \leq c \text { length } ( C )$$ ; confidence 0.985
; $$( D ) \leq c \text { length } ( C )$$ ; confidence 0.985
63. 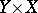 ; $$Y \times X$$ ; confidence 0.869
; $$Y \times X$$ ; confidence 0.869
64. 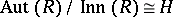 ; $$\operatorname { Aut } ( R ) / \operatorname { ln } n ( R ) \cong H$$ ; confidence 0.228
; $$\operatorname { Aut } ( R ) / \operatorname { ln } n ( R ) \cong H$$ ; confidence 0.228
65. 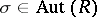 ; $$\sigma \in \operatorname { Aut } ( R )$$ ; confidence 0.958
; $$\sigma \in \operatorname { Aut } ( R )$$ ; confidence 0.958
66. 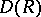 ; $$D ( R )$$ ; confidence 0.960
; $$D ( R )$$ ; confidence 0.960
67. 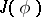 ; $$J ( \phi )$$ ; confidence 0.976
; $$J ( \phi )$$ ; confidence 0.976
68. 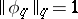 ; $$\| \phi _ { q } \| _ { q } = 1$$ ; confidence 0.797
; $$\| \phi _ { q } \| _ { q } = 1$$ ; confidence 0.797
69. 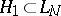 ; $$H _ { 1 } \subset L _ { N }$$ ; confidence 0.459
; $$H _ { 1 } \subset L _ { N }$$ ; confidence 0.459
70. 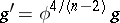 ; $$g ^ { \prime } = \phi ^ { 4 / ( n - 2 ) } g$$ ; confidence 0.828
; $$g ^ { \prime } = \phi ^ { 4 / ( n - 2 ) } g$$ ; confidence 0.828
71. 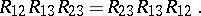 ; $$R _ { 12 } R _ { 13 } R _ { 23 } = R _ { 23 } R _ { 13 } R _ { 12 }$$ ; confidence 0.996
; $$R _ { 12 } R _ { 13 } R _ { 23 } = R _ { 23 } R _ { 13 } R _ { 12 }$$ ; confidence 0.996
72.  ; $$R : X \times X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$$ ; confidence 0.794
; $$R : X \times X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$$ ; confidence 0.794
73. 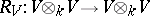 ; $$R _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$$ ; confidence 0.786
; $$R _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$$ ; confidence 0.786
74. 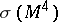 ; $$\sigma ( M ^ { 4 } )$$ ; confidence 1.000
; $$\sigma ( M ^ { 4 } )$$ ; confidence 1.000
75. 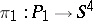 ; $$\pi _ { 1 } : P _ { 1 } \rightarrow S ^ { 4 }$$ ; confidence 0.998
; $$\pi _ { 1 } : P _ { 1 } \rightarrow S ^ { 4 }$$ ; confidence 0.998
76. 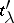 ; $$t _ { \lambda } ^ { \prime }$$ ; confidence 0.881
; $$t _ { \lambda } ^ { \prime }$$ ; confidence 0.881
77. 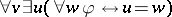 ; $$\forall v \exists u ( \forall w \varphi \leftrightarrow u = w )$$ ; confidence 0.569
; $$\forall v \exists u ( \forall w \varphi \leftrightarrow u = w )$$ ; confidence 0.569
78. 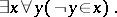 ; $$\forall y ( \neg y \in x )$$ ; confidence 0.930
; $$\forall y ( \neg y \in x )$$ ; confidence 0.930
79. 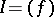 ; $$I = ( f )$$ ; confidence 0.997
; $$I = ( f )$$ ; confidence 0.997
80. 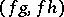 ; $$( f g f h )$$ ; confidence 0.723
; $$( f g f h )$$ ; confidence 0.723
81. 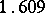 ; $$1.609$$ ; confidence 0.997
; $$1.609$$ ; confidence 0.997
82. 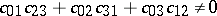 ; $$001 c 23 + c 02 c 31 + c 03 c 12 \neq 0$$ ; confidence 0.156
; $$001 c 23 + c 02 c 31 + c 03 c 12 \neq 0$$ ; confidence 0.156
83.  ; $$x _ { 2 } = r \operatorname { sin } \theta$$ ; confidence 0.977
; $$x _ { 2 } = r \operatorname { sin } \theta$$ ; confidence 0.977
Maximilian Janisch/latexlist/latex/11. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/latex/11&oldid=43829