User:Maximilian Janisch/latexlist/latex
From Encyclopedia of Mathematics
All known classifications:
List
- 41 duplicate(s) ;
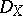; $D x$ ; confidence 0.7125899824424232 - 14 duplicate(s) ;
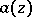; $a ( z )$ ; confidence 0.9482394098353333 - 6 duplicate(s) ;
; $D _ { p }$ ; confidence 0.949111588895238 - 6 duplicate(s) ;
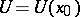; $U = U ( x _ { 0 } )$ ; confidence 0.9908562078219828 - 6 duplicate(s) ;
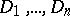; $D _ { 1 } , \ldots , D _ { n }$ ; confidence 0.4988053123602627 - 5 duplicate(s) ;
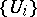; $\{ U _ { i } \}$ ; confidence 0.9836893369850943 - 5 duplicate(s) ;
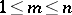; $1 < m \leq n$ ; confidence 0.7369614629370724 - 4 duplicate(s) ;
; $x \in J$ ; confidence 0.9080545659315307 - 3 duplicate(s) ;
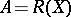; $A = R ( X )$ ; confidence 0.9881159073610419 - 3 duplicate(s) ;
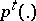; $p ^ { t } ( . )$ ; confidence 0.8165592987790539 - 3 duplicate(s) ;
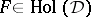; $F \in Hol ( D )$ ; confidence 0.8050535485710892 - 3 duplicate(s) ;
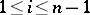; $1 \leq i \leq n - 1$ ; confidence 0.9934317899899957 - 3 duplicate(s) ;
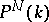; $P ^ { N } ( k )$ ; confidence 0.9987133323048683 - 2 duplicate(s) ;
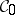; $C _ { 0 }$ ; confidence 0.8004815244538365 - 2 duplicate(s) ;
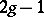; $2 g - 1$ ; confidence 0.9989153310543109 - 2 duplicate(s) ;
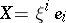; $X = \xi ^ { i }$ ; confidence 0.6624091170439768 - 2 duplicate(s) ;
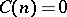; $C ( n ) = 0$ ; confidence 0.9997444185828339 - 2 duplicate(s) ;
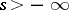; $s > - \infty$ ; confidence 0.9845208310112613 - 1 duplicate(s) ;
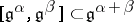; $[ \mathfrak { g } ^ { \alpha } , \mathfrak { g } ^ { \beta } ] \subset \mathfrak { g } ^ { \alpha + \beta }$ ; confidence 0.9810343462221086 - 1 duplicate(s) ;
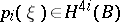; $p _ { i } ( \xi ) \in H ^ { 4 i } ( B )$ ; confidence 0.99791358427467 - 1 duplicate(s) ;
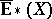; $\overline { E } * ( X )$ ; confidence 0.5537829111373315 - 1 duplicate(s) ;
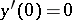; $y ^ { \prime } ( 0 ) = 0$ ; confidence 0.9903064442155347 - 1 duplicate(s) ;
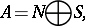; $A = N \oplus s$ ; confidence 0.5210690864049642 - 1 duplicate(s) ;
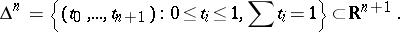; $\Delta ^ { n } = \{ ( t _ { 0 } , \ldots , t _ { k } + 1 ) : 0 \leq t _ { i } \leq 1 , \sum t _ { i } = 1 \} \subset R ^ { n + 1 }$ ; confidence 0.11326702391691568 - 1 duplicate(s) ;
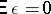; $\overline { \Xi } \epsilon = 0$ ; confidence 0.3260247782643509 - 1 duplicate(s) ;
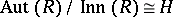; $\operatorname { Aut } ( R ) / \operatorname { ln } n ( R ) \cong H$ ; confidence 0.22810850082016165 - 1 duplicate(s) ;
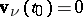; $v _ { \nu } ( t _ { 0 } ) = 0$ ; confidence 0.9958144597610641 - 1 duplicate(s) ;
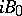; $i B _ { 0 }$ ; confidence 0.9980735616545853 - 1 duplicate(s) ;
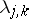; $\lambda _ { j , k }$ ; confidence 0.9635983039923848 - 1 duplicate(s) ;
; $\frac { x ^ { \rho + 1 } f ( x ) } { \int _ { x } ^ { x } t ^ { \sigma } f ( t ) d t } \rightarrow \sigma + \rho + 1 \quad ( x \rightarrow \infty )$ ; confidence 0.3200898597640655 - 1 duplicate(s) ;
; $x > y > z$ ; confidence 0.9993955133881784 - 1 duplicate(s) ;
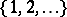; $\{ 1,2 , \dots \}$ ; confidence 0.5933353086312023 - 1 duplicate(s) ;
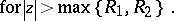; $| z | > \operatorname { max } \{ R _ { 1 } , R _ { 2 } \}$ ; confidence 0.3553260162210176 - 1 duplicate(s) ;
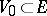; $V _ { 0 } \subset E$ ; confidence 0.9785935677225964 - 1 duplicate(s) ;
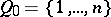; $Q _ { 0 } = \{ 1 , \dots , n \}$ ; confidence 0.774493022175851 - 1 duplicate(s) ;
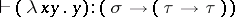; $+ ( \lambda x y \cdot y ) : ( \sigma \rightarrow ( \tau \rightarrow \tau ) )$ ; confidence 0.26240483068240167 - 1 duplicate(s) ;
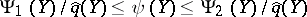; $\Psi _ { 1 } ( Y ) / \hat { q } ( Y ) \leq \psi ( Y ) \leq \Psi _ { 2 } ( Y ) / \hat { q } ( Y )$ ; confidence 0.23609599825199817 - 1 duplicate(s) ;
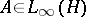; $A \in L _ { \infty } ( H )$ ; confidence 0.9935492544546415 - 1 duplicate(s) ;
; $F _ { A } = * D _ { A } \phi$ ; confidence 0.7384051116139154 - 1 duplicate(s) ;
; $x \in K$ ; confidence 0.6579697488518514 - 1 duplicate(s) ;
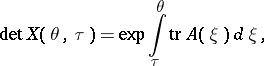; $\operatorname { det } X ( \theta , \tau ) = \operatorname { exp } \int ^ { \theta } \operatorname { tr } A ( \xi ) d \xi$ ; confidence 0.8011337035503415 - 1 duplicate(s) ;
; $z ( 1 - z ) w ^ { \prime \prime } + [ \gamma - ( \alpha + \beta + 1 ) z ] w ^ { \prime } - \alpha \beta w = 0$ ; confidence 0.9956682138248338 - 1 duplicate(s) ;
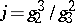; $j = g ^ { 3 } / g ^ { 2 }$ ; confidence 0.7991474537469944 - 1 duplicate(s) ;
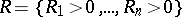; $R = \{ R _ { 1 } > 0 , \dots , R _ { n } > 0 \}$ ; confidence 0.5913209005341337 - 1 duplicate(s) ;
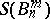; $S ( B _ { n } ^ { m } )$ ; confidence 0.7188991353542298 - 1 duplicate(s) ;
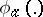; $\phi _ { \mathscr { A } } ( . )$ ; confidence 0.19347190705537826 - 1 duplicate(s) ;
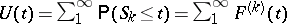; $U ( t ) = \sum _ { 1 } ^ { \infty } P ( S _ { k } \leq t ) = \sum _ { 1 } ^ { \infty } F ^ { ( k ) } ( t )$ ; confidence 0.9173784852068905 - 1 duplicate(s) ;
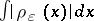; $\int | \rho _ { \varepsilon } ( x ) | d x$ ; confidence 0.964771564499889 - 1 duplicate(s) ;
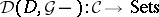; $D ( D , G - ) : C \rightarrow$ ; confidence 0.39755631559394916 - 1 duplicate(s) ;
; $Q / Z$ ; confidence 0.663649051291889 - 1 duplicate(s) ;
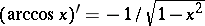; $( \operatorname { arccos } x ) ^ { \prime } = - 1 / \sqrt { 1 - x ^ { 2 } }$ ; confidence 0.9962210404610826 - 1 duplicate(s) ;
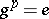; $g ^ { p } = e$ ; confidence 0.9783864254422098 - 1 duplicate(s) ;
; $\rho _ { M _ { 1 } } ( X , Y ) \geq \rho _ { M _ { 2 } } ( \phi ( X ) , \phi ( Y ) )$ ; confidence 0.6746325376340707 - 1 duplicate(s) ;
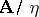; $A / \eta$ ; confidence 0.7016005337400021 - 1 duplicate(s) ;
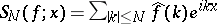; $S _ { N } ( f ; x ) = \sum _ { k | \leq N } \hat { f } ( k ) e ^ { i k x }$ ; confidence 0.6326879749735163 - 1 duplicate(s) ;
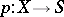; $p : X \rightarrow S$ ; confidence 0.9979840368620039 - 1 duplicate(s) ;
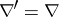; $\nabla ^ { \prime } = \nabla$ ; confidence 0.998307629684964 - 1 duplicate(s) ;
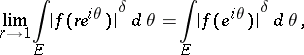; $\operatorname { lim } _ { r \rightarrow 1 } \int _ { E } | f ( r e ^ { i \theta } ) | ^ { \delta } d \theta = \int _ { E } | f ( e ^ { i \theta } ) | ^ { \delta } d \theta$ ; confidence 0.9636735762236702 - 1 duplicate(s) ;
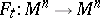; $F _ { t } : M ^ { n } \rightarrow M ^ { n }$ ; confidence 0.9892303983467674 - 1 duplicate(s) ;
; $V ( \Lambda ^ { \prime } ) \otimes V ( \Lambda ^ { \prime \prime } )$ ; confidence 0.9956682193198153 - 1 duplicate(s) ;
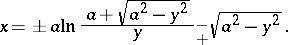; $x = \pm \alpha \operatorname { ln } \frac { \alpha + \sqrt { \alpha ^ { 2 } - y ^ { 2 } } } { y } - \sqrt { \alpha ^ { 2 } - y ^ { 2 } }$ ; confidence 0.3913006402000813 - 1 duplicate(s) ;
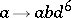; $a \rightarrow a b d ^ { 6 }$ ; confidence 0.5686678070129293 - 1 duplicate(s) ;
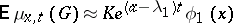; $E \mu _ { X , t } ( G ) \approx K e ^ { ( \alpha - \lambda _ { 1 } ) t } \phi _ { 1 } ( x )$ ; confidence 0.2070610832487361 - 1 duplicate(s) ;
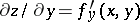; $\partial z / \partial y = f ^ { \prime } ( x , y )$ ; confidence 0.43958333682472145 - 1 duplicate(s) ;
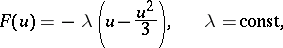; $F ( u ) = - \lambda ( u - \frac { u ^ { 2 } } { 3 } ) , \quad \lambda =$ ; confidence 0.7430177844611311 - 1 duplicate(s) ;
; $\dot { x } ( t ) = f ( t , x _ { t } )$ ; confidence 0.5429682760018246 - 1 duplicate(s) ;
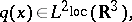; $q ( x ) \in L ^ { 2 } \operatorname { loc } ( R ^ { 3 } )$ ; confidence 0.9533661981123269 - 1 duplicate(s) ;
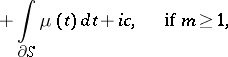; $+ \int _ { \partial S } \mu ( t ) d t + i c , \quad \text { if } m \geq 1$ ; confidence 0.9868991488845216 - 1 duplicate(s) ;
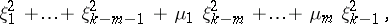; $\xi _ { 1 } ^ { 2 } + \ldots + \xi _ { k - m - 1 } ^ { 2 } + \mu _ { 1 } \xi _ { k - m } ^ { 2 } + \ldots + \mu _ { m } \xi _ { k - 1 } ^ { 2 }$ ; confidence 0.818133040173671 - 1 duplicate(s) ;
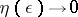; $\eta ( \epsilon ) \rightarrow 0$ ; confidence 0.9930945383534938 - 1 duplicate(s) ;
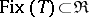; $\operatorname { Fix } ( T ) \subset \mathfrak { R }$ ; confidence 0.7097136892515409 - 1 duplicate(s) ;
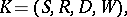; $K = ( S , R , D , W )$ ; confidence 0.9948102230937678 - 1 duplicate(s) ;
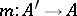; $m : A ^ { \prime } \rightarrow A$ ; confidence 0.9973560859607404 - 1 duplicate(s) ;
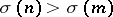; $\sigma ( n ) > \sigma ( m )$ ; confidence 0.995848659246317 - 1 duplicate(s) ;
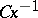; $C x ^ { - 1 }$ ; confidence 0.8338278081003673 - 1 duplicate(s) ;
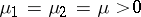; $\mu _ { 1 } = \mu _ { 2 } = \mu > 0$ ; confidence 0.9998340722154501 - 1 duplicate(s) ;
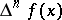; $\Delta ^ { n } f ( x )$ ; confidence 0.9761551779890966 - 1 duplicate(s) ;
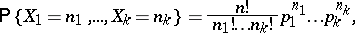; $P \{ X _ { 1 } = n _ { 1 } , \dots , X _ { k } = n _ { k } \} = \frac { n ! } { n ! \cdots n _ { k } ! } p _ { 1 } ^ { n _ { 1 } } \dots p _ { k } ^ { n _ { k } }$ ; confidence 0.054218093847858334 - 1 duplicate(s) ;
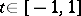; $t \in [ - 1,1 ]$ ; confidence 0.9658081901466191 - 1 duplicate(s) ;
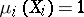; $\mu _ { i } ( X _ { i } ) = 1$ ; confidence 0.9902724405115619 - 1 duplicate(s) ;
; Missing ; confidence 0 - 1 duplicate(s) ;
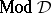; $D$ ; confidence 0.9836142568793015 - 1 duplicate(s) ;
; $m _ { G } = D ( u ) / 2 \pi$ ; confidence 0.8112748700162913 - 1 duplicate(s) ;
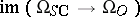; $im ( \Omega _ { S C } \rightarrow \Omega _ { O } )$ ; confidence 0.23040392825448733 - 1 duplicate(s) ;
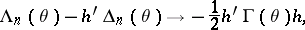; $\Lambda _ { n } ( \theta ) - h ^ { \prime } \Delta _ { n } ( \theta ) \rightarrow - \frac { 1 } { 2 } h ^ { \prime } \Gamma ( \theta ) h$ ; confidence 0.8428428443145696 - 1 duplicate(s) ;
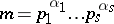; $m = p _ { 1 } ^ { \alpha _ { 1 } } \ldots p _ { s } ^ { \alpha _ { S } }$ ; confidence 0.46249649812198196 - 1 duplicate(s) ;
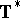; $T ^ { * }$ ; confidence 0.9844626718823335 - 1 duplicate(s) ;
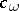; $C _ { \omega }$ ; confidence 0.07294451014735373 - 1 duplicate(s) ;
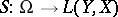; $S : \Omega \rightarrow L ( Y , X )$ ; confidence 0.9939321146895647 - 1 duplicate(s) ;
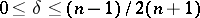; $0 \leq \delta \leq ( n - 1 ) / 2 ( n + 1 )$ ; confidence 0.9985895509258916 - 1 duplicate(s) ;
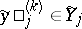; $\tilde { Y } \square _ { j } ^ { ( k ) } \in Y _ { j }$ ; confidence 0.17197034114794676 - 1 duplicate(s) ;
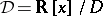; $D = R [ x ] / D$ ; confidence 0.9679769594271714 - 1 duplicate(s) ;
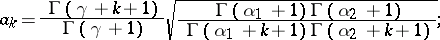; $\alpha _ { k } = \frac { \Gamma ( \gamma + k + 1 ) } { \Gamma ( \gamma + 1 ) } \sqrt { \frac { \Gamma ( \alpha _ { 1 } + 1 ) \Gamma ( \alpha _ { 2 } + 1 ) } { \Gamma ( \alpha _ { 1 } + k + 1 ) \Gamma ( \alpha _ { 2 } + k + 1 ) } }$ ; confidence 0.9041210547693775 - 1 duplicate(s) ;
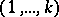; $( 1 , \dots , k )$ ; confidence 0.7759125219520806 - 1 duplicate(s) ;
; Missing ; confidence 0 - 1 duplicate(s) ;
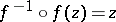; $f ^ { - 1 } \circ f ( z ) = z$ ; confidence 0.9863835099245214 - 1 duplicate(s) ;
; $\Sigma _ { S }$ ; confidence 0.7602855286138045 - 1 duplicate(s) ;
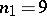; $n _ { 1 } = 9$ ; confidence 0.8217276068104418 - 1 duplicate(s) ;
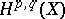; $H ^ { p , q } ( X )$ ; confidence 0.9128683228703054 - 1 duplicate(s) ;
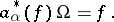; $\alpha _ { \alpha } ^ { * } ( f ) \Omega = f$ ; confidence 0.9617933295666078 - 1 duplicate(s) ;
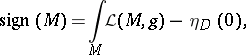; $\operatorname { sign } ( M ) = \int _ { M } L ( M , g ) - \eta _ { D } ( 0 )$ ; confidence 0.9583030996297096 - 1 duplicate(s) ;
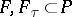; $F , F _ { \tau } \subset P$ ; confidence 0.9767753813241717 - 1 duplicate(s) ;
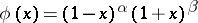; $\phi ( x ) = ( 1 - x ) ^ { \alpha } ( 1 + x ) ^ { \beta }$ ; confidence 0.9976319244241609 - 1 duplicate(s) ;
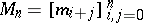; $M _ { n } = [ m _ { i } + j ] _ { i , j } ^ { n } = 0$ ; confidence 0.46928897388284957 - 1 duplicate(s) ;
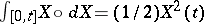; $\int [ 0 , t ] X \circ d X = ( 1 / 2 ) X ^ { 2 } ( t )$ ; confidence 0.6980818282530422 - 1 duplicate(s) ;
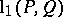; $l _ { 1 } ( P , Q )$ ; confidence 0.6109194252117595 - 1 duplicate(s) ;
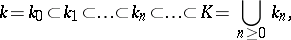; $k = k _ { 0 } \subset k _ { 1 } \subset \ldots \subset k _ { n } \subset \ldots \subset K = \cup _ { n \geq 0 } k _ { k }$ ; confidence 0.43410160727313885 - 1 duplicate(s) ;
; $K . ( H X ) = ( K H ) X$ ; confidence 0.7659737865659941 - 1 duplicate(s) ;
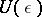; $U ( \epsilon )$ ; confidence 0.9981553778972309 - 1 duplicate(s) ;
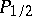; $P _ { 1 / 2 }$ ; confidence 0.9956493318117914 - 1 duplicate(s) ;
; $\phi \in H$ ; confidence 0.9809538776286444 - 1 duplicate(s) ;
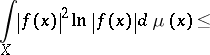; $\int _ { X } | f ( x ) | ^ { 2 } \operatorname { ln } | f ( x ) | d \mu ( x ) \leq$ ; confidence 0.9895172018375741 - 1 duplicate(s) ;
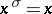; $x ^ { \sigma } = x$ ; confidence 0.9478216561987443 - 1 duplicate(s) ;
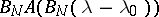; $B _ { N } A ( B _ { N } ( \lambda - \lambda _ { 0 } ) )$ ; confidence 0.980198148600406 - 1 duplicate(s) ;
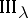; $\Pi I _ { \lambda }$ ; confidence 0.2996377272936826 - 1 duplicate(s) ;
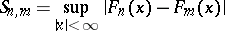; $S _ { x , m } = \operatorname { sup } _ { | x | < \infty } | F _ { n } ( x ) - F _ { m } ( x ) |$ ; confidence 0.2014066318219743 - 1 duplicate(s) ;
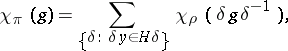; $\chi _ { \pi } ( g ) = \sum _ { \{ \delta : \delta y \in H \delta \} } \chi _ { \rho } ( \delta g \delta ^ { - 1 } )$ ; confidence 0.902751217861617 - 1 duplicate(s) ;
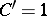; $C ^ { \prime } = 1$ ; confidence 0.9986067312742835 - 1 duplicate(s) ;
; $X = N ( A ) + X , \quad Y = Z + R ( A )$ ; confidence 0.9876165622757166 - 1 duplicate(s) ;
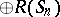; $\oplus R ( S _ { n } )$ ; confidence 0.9053981209446474 - 1 duplicate(s) ;
; $1 \leq u \leq 2$ ; confidence 0.97632096204764 - 1 duplicate(s) ;
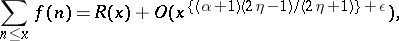; $\sum _ { n < x } f ( n ) = R ( x ) + O ( x ^ { \{ ( \alpha + 1 ) ( 2 \eta - 1 ) / ( 2 \eta + 1 ) \} + \epsilon } )$ ; confidence 0.7947232878891592 - 1 duplicate(s) ;
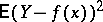; $E ( Y - f ( x ) ) ^ { 2 }$ ; confidence 0.5470389324901368 - 1 duplicate(s) ;
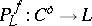; $P _ { I } ^ { f } : C ^ { \infty } \rightarrow L$ ; confidence 0.32143585152427034 - 1 duplicate(s) ;
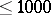; $< 1$ ; confidence 0.9989134216768655
How to Cite This Entry:
Maximilian Janisch/latexlist/latex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/latex&oldid=43762
Maximilian Janisch/latexlist/latex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/latex&oldid=43762