User:Maximilian Janisch/latexlist
Quoting from EoM talk: "This project is based on an electronic version of the 'Encyclopaedia of Mathematics', published by Kluwer Academic Publishers until 2003, and by Springer after that. The encyclopaedia goes back to the Soviet Matematicheskaya entsiklopediya (1977), originally edited by Ivan Matveevich Vinogradov. The electronic version had its formulae written in TEX, which were saved as png images. On its way through the various publishers the original TEX source code was lost, therefore, to edit a formula in one of these original pages requires to retype the code for that formula from scratch.
For the project, it will be of big help to transcribe the old pages. To make this easy, it was decided to use MathJax, which allows to use Plain TEX or LATEX for formulae encoding. "
Currently, there are about 270'000 images of formulas whoms LaTeX source code has been lost. Many of these images are duplicates (see User:Maximilian Janisch/latexlist/duplicates), which makes classification easier. There are services such as Mathpix which automatically transform the images back to TEX code. However, these translations are not infallible (see below).
Currently, I have classified all 270'125 images of this Encyclopedia into 103'285 classes of duplicates (some images appear hundreds of times, others just once). My goal is to translate all 103'285 images back to TEX code with the help of Mathpix, and then replace every image in the articles by its corresponding TEX code.
List
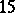 : $15$
(confidence 1.00)
: $15$
(confidence 1.00)
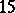 : $15$
(confidence 1.00)
: $15$
(confidence 1.00)
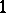 : $1$
(confidence 1.00)
: $1$
(confidence 1.00)
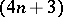 : $( 4 n + 3 )$
(confidence 1.00)
: $( 4 n + 3 )$
(confidence 1.00)
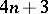 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
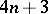 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
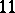 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
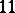 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
 : $2$
(confidence 1.00)
: $2$
(confidence 1.00)
 : $2$
(confidence 1.00)
: $2$
(confidence 1.00)
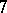 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
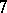 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
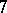 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
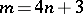 : $m = 4 n + 3$
(confidence 1.00)
: $m = 4 n + 3$
(confidence 1.00)
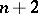 : $n + 2$
(confidence 1.00)
: $n + 2$
(confidence 1.00)
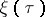 : $\xi ( \tau )$
(confidence 1.00)
: $\xi ( \tau )$
(confidence 1.00)
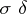 : $\sigma \delta$
(confidence 1.00)
: $\sigma \delta$
(confidence 1.00)
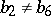 : $b _ { 2 } \neq b _ { 6 }$
(confidence 1.00)
: $b _ { 2 } \neq b _ { 6 }$
(confidence 1.00)
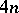 : $4 n$
(confidence 1.00)
: $4 n$
(confidence 1.00)
 : $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 1.00)
: $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 1.00)
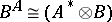 : $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
: $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
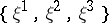 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
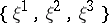 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
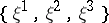 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
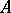 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
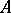 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
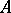 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
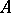 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
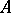 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
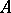 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
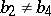 : $b _ { 2 } \neq b _ { 4 }$
(confidence 1.00)
: $b _ { 2 } \neq b _ { 4 }$
(confidence 1.00)
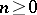 : $n \geq 0$
(confidence 1.00)
: $n \geq 0$
(confidence 1.00)
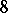 : $8$
(confidence 0.99)
: $8$
(confidence 0.99)
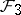 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
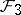 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
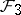 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
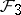 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
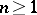 : $n \geq 1$
(confidence 0.99)
: $n \geq 1$
(confidence 0.99)
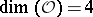 : $\operatorname { dim } ( O ) = 4$
(confidence 0.99)
: $\operatorname { dim } ( O ) = 4$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $z$
(confidence 0.99)
: $z$
(confidence 0.99)
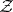 : $z$
(confidence 0.99)
: $z$
(confidence 0.99)
 : $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.98)
: $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.98)
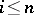 : $i < n$
(confidence 0.98)
: $i < n$
(confidence 0.98)
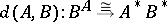 : $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.98)
: $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.98)
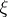 : $\xi$
(confidence 0.98)
: $\xi$
(confidence 0.98)
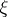 : $\xi$
(confidence 0.98)
: $\xi$
(confidence 0.98)
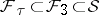 : $F _ { \tau } \subset F _ { 3 } \subset S$
(confidence 0.97)
: $F _ { \tau } \subset F _ { 3 } \subset S$
(confidence 0.97)
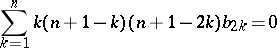 : $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.96)
: $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.96)
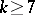 : $k > 7$
(confidence 0.96)
: $k > 7$
(confidence 0.96)
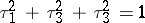 : $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.96)
: $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.96)
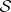 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
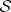 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
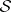 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
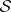 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
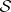 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
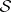 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
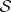 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
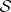 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
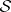 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
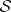 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
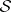 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
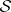 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
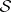 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
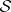 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
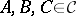 : $A , B , C \in C$
(confidence 0.95)
: $A , B , C \in C$
(confidence 0.95)
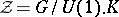 : $Z = G / U ( 1 ) . K$
(confidence 0.95)
: $Z = G / U ( 1 ) . K$
(confidence 0.95)
 : $> 7$
(confidence 0.95)
: $> 7$
(confidence 0.95)
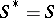 : $S ^ { * } = S$
(confidence 0.95)
: $S ^ { * } = S$
(confidence 0.95)
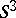 : $5 ^ { 3 }$
(confidence 0.94)
: $5 ^ { 3 }$
(confidence 0.94)
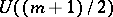 : $U ( ( m + 1 ) / 2 )$
(confidence 0.94)
: $U ( ( m + 1 ) / 2 )$
(confidence 0.94)
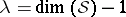 : $\lambda = \operatorname { dim } ( S ) - 1$
(confidence 0.94)
: $\lambda = \operatorname { dim } ( S ) - 1$
(confidence 0.94)
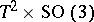 : $T ^ { 2 } \times SO ( 3 )$
(confidence 0.94)
: $T ^ { 2 } \times SO ( 3 )$
(confidence 0.94)
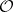 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
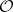 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
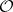 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
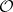 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
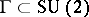 : $\Gamma \subset \operatorname { SU } ( 2 )$
(confidence 0.92)
: $\Gamma \subset \operatorname { SU } ( 2 )$
(confidence 0.92)
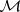 : $M$
(confidence 0.92)
: $M$
(confidence 0.92)
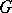 : $G$
(confidence 0.92)
: $G$
(confidence 0.92)
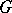 : $G$
(confidence 0.92)
: $G$
(confidence 0.92)
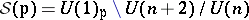 : $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.92)
: $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.92)
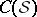 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
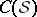 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
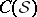 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
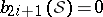 : $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.90)
: $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.90)
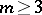 : $m > 3$
(confidence 0.89)
: $m > 3$
(confidence 0.89)
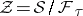 : $Z = S / F _ { \tau }$
(confidence 0.89)
: $Z = S / F _ { \tau }$
(confidence 0.89)
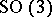 : $SO ( 3 )$
(confidence 0.88)
: $SO ( 3 )$
(confidence 0.88)
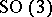 : $SO ( 3 )$
(confidence 0.88)
: $SO ( 3 )$
(confidence 0.88)
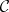 : $C$
(confidence 0.87)
: $C$
(confidence 0.87)
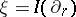 : $\xi = I ( \partial _ { r } )$
(confidence 0.87)
: $\xi = I ( \partial _ { r } )$
(confidence 0.87)
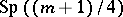 : $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.86)
: $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.86)
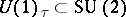 : $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.82)
: $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.82)
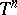 : $T ^ { n }$
(confidence 0.82)
: $T ^ { n }$
(confidence 0.82)
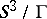 : $S ^ { 3 } / \Gamma$
(confidence 0.82)
: $S ^ { 3 } / \Gamma$
(confidence 0.82)
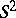 : $5 ^ { 2 }$
(confidence 0.80)
: $5 ^ { 2 }$
(confidence 0.80)
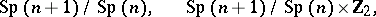 : $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times Z _ { 2 }$
(confidence 0.80)
: $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times Z _ { 2 }$
(confidence 0.80)
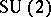 : $SU ( 2 )$
(confidence 0.79)
: $SU ( 2 )$
(confidence 0.79)
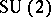 : $SU ( 2 )$
(confidence 0.79)
: $SU ( 2 )$
(confidence 0.79)
 : $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.79)
: $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.79)
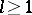 : $l > 1$
(confidence 0.77)
: $l > 1$
(confidence 0.77)
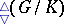 : $\triangle ( G / K )$
(confidence 0.77)
: $\triangle ( G / K )$
(confidence 0.77)
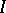 : $1$
(confidence 0.77)
: $1$
(confidence 0.77)
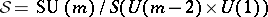 : $S = SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$
(confidence 0.75)
: $S = SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$
(confidence 0.75)
 : $5$
(confidence 0.74)
: $5$
(confidence 0.74)
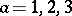 : $\alpha = 1,2,3$
(confidence 0.74)
: $\alpha = 1,2,3$
(confidence 0.74)
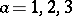 : $\alpha = 1,2,3$
(confidence 0.74)
: $\alpha = 1,2,3$
(confidence 0.74)
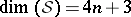 : $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.73)
: $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.73)
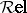 : $R e l$
(confidence 0.69)
: $R e l$
(confidence 0.69)
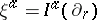 : $\xi ^ { \alpha } = I ^ { \alpha } ( \partial _ { r } )$
(confidence 0.67)
: $\xi ^ { \alpha } = I ^ { \alpha } ( \partial _ { r } )$
(confidence 0.67)
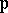 : $p$
(confidence 0.64)
: $p$
(confidence 0.64)
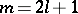 : $m = 2 l + 1$
(confidence 0.61)
: $m = 2 l + 1$
(confidence 0.61)
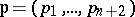 : $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.61)
: $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.61)
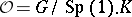 : $O = G / Sp ( 1 ) . K$
(confidence 0.57)
: $O = G / Sp ( 1 ) . K$
(confidence 0.57)
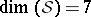 : $\operatorname { lim } ( S ) = 7$
(confidence 0.53)
: $\operatorname { lim } ( S ) = 7$
(confidence 0.53)
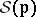 : $S ( p )$
(confidence 0.52)
: $S ( p )$
(confidence 0.52)
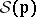 : $S ( p )$
(confidence 0.52)
: $S ( p )$
(confidence 0.52)
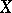 : $X$
(confidence 0.51)
: $X$
(confidence 0.51)
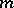 : $m$
(confidence 0.50)
: $m$
(confidence 0.50)
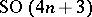 : $SO ( 4 n + 3 )$
(confidence 0.49)
: $SO ( 4 n + 3 )$
(confidence 0.49)
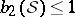 : $b _ { 2 } ( S ) \leq 1$
(confidence 0.48)
: $b _ { 2 } ( S ) \leq 1$
(confidence 0.48)
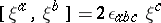 : $[ \xi ^ { \alpha } , \xi ^ { b } ] = 2 \epsilon _ { \alpha b c } \xi ^ { c }$
(confidence 0.47)
: $[ \xi ^ { \alpha } , \xi ^ { b } ] = 2 \epsilon _ { \alpha b c } \xi ^ { c }$
(confidence 0.47)
 : $sp ( 0 )$
(confidence 0.44)
: $sp ( 0 )$
(confidence 0.44)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.39)
: $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.39)
 : $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.37)
: $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.37)
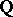 : $5$
(confidence 0.36)
: $5$
(confidence 0.36)
 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
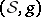 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
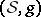 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
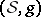 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
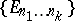 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
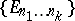 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
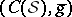 : $( C ( s ) , g )$
(confidence 0.28)
: $( C ( s ) , g )$
(confidence 0.28)
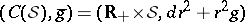 : $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.27)
: $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.27)
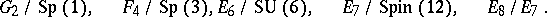 : $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$
(confidence 0.27)
: $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$
(confidence 0.27)
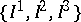 : $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$
(confidence 0.26)
: $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$
(confidence 0.26)
 : $\{ A _ { n _ { 1 } } \ldots n _ { k } \}$
(confidence 0.24)
: $\{ A _ { n _ { 1 } } \ldots n _ { k } \}$
(confidence 0.24)
 : $g ( \xi ^ { d } , \xi ^ { b } ) = \delta _ { c t b }$
(confidence 0.22)
: $g ( \xi ^ { d } , \xi ^ { b } ) = \delta _ { c t b }$
(confidence 0.22)
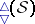 : $\triangle ( S )$
(confidence 0.20)
: $\triangle ( S )$
(confidence 0.20)
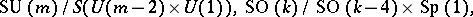 : $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times Sp ( 1 )$
(confidence 0.19)
: $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times Sp ( 1 )$
(confidence 0.19)
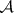 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
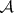 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
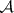 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
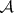 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
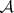 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
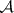 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
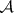 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
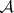 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
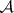 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
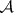 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
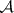 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
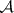 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
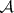 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
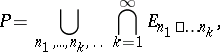 : $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } \square \ldots n _ { k } }$
(confidence 0.16)
: $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } \square \ldots n _ { k } }$
(confidence 0.16)
 : $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.14)
: $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.14)
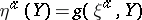 : $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$
(confidence 0.06)
: $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$
(confidence 0.06)
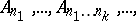 : $_ { 1 } , \ldots , A _ { k _ { 1 } } \ldots n _ { k } , \dots ,$
(confidence 0.06)
: $_ { 1 } , \ldots , A _ { k _ { 1 } } \ldots n _ { k } , \dots ,$
(confidence 0.06)
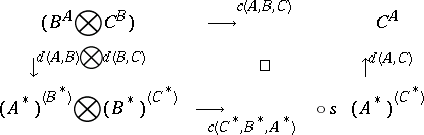 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
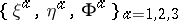 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
Maximilian Janisch/latexlist. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist&oldid=43756