User:Maximilian Janisch/latexlist
This is a list of automatically classified LaTeX files. You can manually edit this list, your changes will currently not be considered and only overwritten though.
List
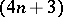 : $( 4 n + 3 )$
(confidence 1.00)
: $( 4 n + 3 )$
(confidence 1.00)
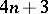 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
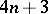 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
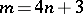 : $m = 4 n + 3$
(confidence 1.00)
: $m = 4 n + 3$
(confidence 1.00)
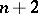 : $n + 2$
(confidence 1.00)
: $n + 2$
(confidence 1.00)
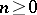 : $n > 0$
(confidence 1.00)
: $n > 0$
(confidence 1.00)
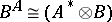 : $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
: $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
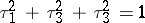 : $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.99)
: $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.99)
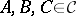 : $A , B , C \in C$
(confidence 0.99)
: $A , B , C \in C$
(confidence 0.99)
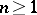 : $n > 1$
(confidence 0.99)
: $n > 1$
(confidence 0.99)
 : $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 0.99)
: $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 0.99)
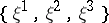 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
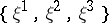 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
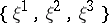 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
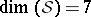 : $( S ) = 7$
(confidence 0.98)
: $( S ) = 7$
(confidence 0.98)
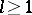 : $> 1$
(confidence 0.98)
: $> 1$
(confidence 0.98)
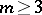 : $m > 3$
(confidence 0.98)
: $m > 3$
(confidence 0.98)
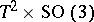 : $T ^ { 2 } \times SO ( 3 )$
(confidence 0.96)
: $T ^ { 2 } \times SO ( 3 )$
(confidence 0.96)
 : $p ( 0$
(confidence 0.93)
: $p ( 0$
(confidence 0.93)
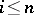 : $i < n$
(confidence 0.92)
: $i < n$
(confidence 0.92)
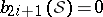 : $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.91)
: $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.91)
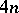 : $4 n$
(confidence 0.90)
: $4 n$
(confidence 0.90)
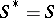 : $S ^ { * } = S$
(confidence 0.90)
: $S ^ { * } = S$
(confidence 0.90)
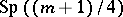 : $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.90)
: $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.90)
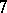 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
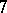 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
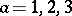 : $a = 1,2,3$
(confidence 0.89)
: $a = 1,2,3$
(confidence 0.89)
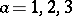 : $a = 1,2,3$
(confidence 0.89)
: $a = 1,2,3$
(confidence 0.89)
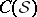 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
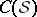 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
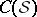 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
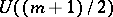 : $U ( ( m + 1 ) / 2 )$
(confidence 0.87)
: $U ( ( m + 1 ) / 2 )$
(confidence 0.87)
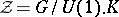 : $Z = G / U ( 1 ) . K$
(confidence 0.85)
: $Z = G / U ( 1 ) . K$
(confidence 0.85)
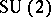 : $U ( 2 )$
(confidence 0.84)
: $U ( 2 )$
(confidence 0.84)
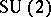 : $U ( 2 )$
(confidence 0.84)
: $U ( 2 )$
(confidence 0.84)
 : $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.81)
: $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.81)
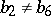 : $b _ { 2 } \neq b _ { 6 }$
(confidence 0.79)
: $b _ { 2 } \neq b _ { 6 }$
(confidence 0.79)
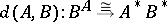 : $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.75)
: $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.75)
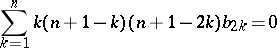 : $\sum ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.74)
: $\sum ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.74)
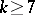 : $x > 7$
(confidence 0.72)
: $x > 7$
(confidence 0.72)
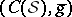 : $C ( s ) , g$
(confidence 0.71)
: $C ( s ) , g$
(confidence 0.71)
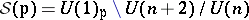 : $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.71)
: $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.71)
 : $> 7$
(confidence 0.68)
: $> 7$
(confidence 0.68)
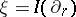 : $\xi = I ( \partial _ { y } )$
(confidence 0.65)
: $\xi = I ( \partial _ { y } )$
(confidence 0.65)
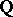 : $4$
(confidence 0.62)
: $4$
(confidence 0.62)
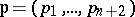 : $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.59)
: $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.59)
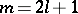 : $m = 2 l + 1$
(confidence 0.59)
: $m = 2 l + 1$
(confidence 0.59)
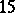 : $1.3$
(confidence 0.59)
: $1.3$
(confidence 0.59)
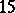 : $1.3$
(confidence 0.59)
: $1.3$
(confidence 0.59)
 : $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.56)
: $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.56)
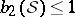 : $( S ) \leq 1$
(confidence 0.54)
: $( S ) \leq 1$
(confidence 0.54)
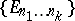 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
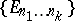 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
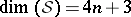 : $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.51)
: $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.51)
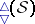 : $\Delta ( S )$
(confidence 0.50)
: $\Delta ( S )$
(confidence 0.50)
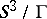 : $S ^ { 3 } / \Gamma$
(confidence 0.50)
: $S ^ { 3 } / \Gamma$
(confidence 0.50)
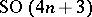 : $S O ( 4 n + 3 )$
(confidence 0.49)
: $S O ( 4 n + 3 )$
(confidence 0.49)
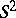 : $5$
(confidence 0.49)
: $5$
(confidence 0.49)
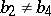 : $b _ { 2 } \neq b$
(confidence 0.48)
: $b _ { 2 } \neq b$
(confidence 0.48)
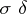 : $\pi$
(confidence 0.45)
: $\pi$
(confidence 0.45)
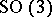 : $0 ( 3$
(confidence 0.45)
: $0 ( 3$
(confidence 0.45)
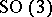 : $0 ( 3$
(confidence 0.45)
: $0 ( 3$
(confidence 0.45)
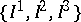 : $\{ I ^ { 1 } , R , \vec { P } \}$
(confidence 0.43)
: $\{ I ^ { 1 } , R , \vec { P } \}$
(confidence 0.43)
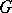 : $x$
(confidence 0.41)
: $x$
(confidence 0.41)
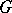 : $x$
(confidence 0.41)
: $x$
(confidence 0.41)
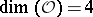 : $( O ) = \mathfrak { L }$
(confidence 0.41)
: $( O ) = \mathfrak { L }$
(confidence 0.41)
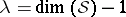 : $1 = \operatorname { dim } ( S ) - 1$
(confidence 0.40)
: $1 = \operatorname { dim } ( S ) - 1$
(confidence 0.40)
 : $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.40)
: $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.40)
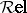 : $\sqrt { 2 } e$
(confidence 0.37)
: $\sqrt { 2 } e$
(confidence 0.37)
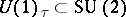 : $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.37)
: $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.37)
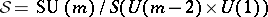 : $S = \operatorname { SU } ( m ) / S ( U ( m - 2 ) \times U ( 1 )$
(confidence 0.36)
: $S = \operatorname { SU } ( m ) / S ( U ( m - 2 ) \times U ( 1 )$
(confidence 0.36)
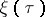 : $= T$
(confidence 0.36)
: $= T$
(confidence 0.36)
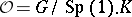 : $O = G / Sp ( 1 ) . K$
(confidence 0.35)
: $O = G / Sp ( 1 ) . K$
(confidence 0.35)
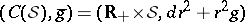 : $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.35)
: $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.35)
 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
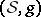 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
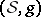 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
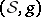 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
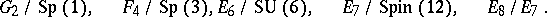 : $\Delta$
(confidence 0.32)
: $\Delta$
(confidence 0.32)
 : $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
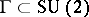 : $\subset \operatorname { SU } ( 2 )$
(confidence 0.30)
: $\subset \operatorname { SU } ( 2 )$
(confidence 0.30)
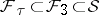 : $F _ { T } \subset F _ { 3 } \subset S$
(confidence 0.30)
: $F _ { T } \subset F _ { 3 } \subset S$
(confidence 0.30)
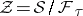 : $Z = S / F _ { T }$
(confidence 0.29)
: $Z = S / F _ { T }$
(confidence 0.29)
 : $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.26)
: $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.26)
 : $\Phi ^ { d t } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.24)
: $\Phi ^ { d t } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.24)
 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
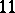 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
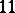 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
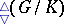 : $\hat { \gamma } ( G / K )$
(confidence 0.22)
: $\hat { \gamma } ( G / K )$
(confidence 0.22)
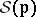 : $S ( D$
(confidence 0.16)
: $S ( D$
(confidence 0.16)
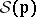 : $S ( D$
(confidence 0.16)
: $S ( D$
(confidence 0.16)
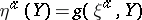 : $\eta ^ { \alpha } ( Y ) = g ( \xi ^ { d : } , Y )$
(confidence 0.15)
: $\eta ^ { \alpha } ( Y ) = g ( \xi ^ { d : } , Y )$
(confidence 0.15)
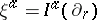 : $\xi ^ { d x } = I ^ { \alpha } ( \partial _ { \gamma } )$
(confidence 0.12)
: $\xi ^ { d x } = I ^ { \alpha } ( \partial _ { \gamma } )$
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
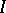 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
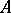 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
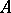 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
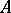 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
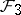 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
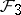 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
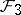 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
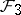 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
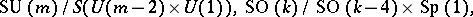 : $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times$
(confidence 0.10)
: $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times$
(confidence 0.10)
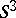 : $5 ^ { 2 }$
(confidence 0.10)
: $5 ^ { 2 }$
(confidence 0.10)
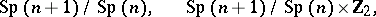 : $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times 2$
(confidence 0.10)
: $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times 2$
(confidence 0.10)
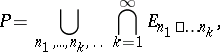 : $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } } \square \ldots x _ { k }$
(confidence 0.10)
: $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } } \square \ldots x _ { k }$
(confidence 0.10)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
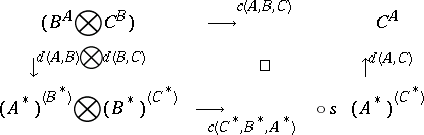 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
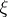 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
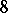 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
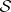 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
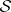 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
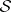 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
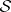 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
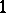 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
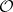 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
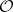 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
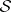 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
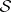 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
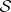 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
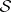 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
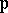 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
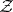 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
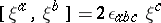 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
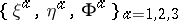 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
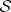 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
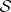 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
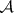 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
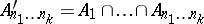 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
Maximilian Janisch/latexlist. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist&oldid=43673