Schwarzian derivative

Schwarz derivative, Schwarzian differential parameter, of an analytic function of a complex variable

The differential expression

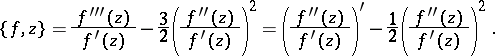It first appeared in studies on conformal mapping of polygons onto the disc, in particular in the studies of H.A. Schwarz [1].

The most important property of the Schwarzian derivative is its invariance under fractional-linear transformations (Möbius transformations) of the function , i.e. if

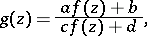then . Applications of the Schwarzian derivative are especially connected with problems on univalent analytic functions. For example, if is a univalent analytic function in the disc , and if , , then

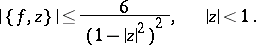Conversely, if is regular in 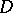and if

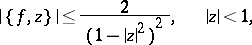then is a univalent function in , and it is impossible in this case to increase the constant 2.

References

[1]	H.A. Schwarz, "Gesamm. math. Abhandl." , 2 , Springer (1890)
[2]	R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

Comments

The necessary and sufficient conditions for univalency in terms of the Schwarzian derivative stated above are due to W. Kraus [a1] and Z. Nehari [a2], respectively; see [a3], pp. 258-265, for further discussion. A nice discussion of the Schwarzian derivative is in [a4], pp. 50-58.

References

[a1]	W. Kraus, "Ueber den Zusammenhang einiger Charakteristiken eines einfach zusammenhängenden Bereiches mit der Kreisabbildung" Mitt. Math. Sem. Giessen , 21 (1932) pp. 1–28
[a2]	Z. Nehari, "The Schwarzian derivative and schlicht functions" Bull. Amer. Math. Soc. , 55 (1949) pp. 545–551
[a3]	P.L. Duren, "Univalent functions" , Springer (1983) pp. 258
[a4]	O. Lehto, "Univalent functions and Teichmüller spaces" , Springer (1987)
[a5]	Z. Nehari, "Conformal mapping" , Dover, reprint (1975) pp. 2