Spectral set

A spectral set of an operator 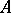on a normed space is a subset 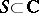such that

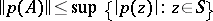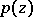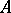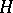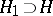for any polynomial . Thus, the unit circle is a spectral set for any contraction (an operator whose norm does not exceed one) on a Hilbert space (von Neumann's theorem). This result is closely connected with the existence of a unitary power dilation for any contraction (a power dilation of an operator on a Hilbert space is defined as an operator on a Hilbert space such that 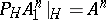, 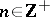); a compact subset 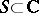is spectral for if and only if 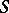has a normal power dilation with spectrum in 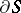. The minimal radius of the circle which is a spectral set for every contraction in a Banach space is equal to one.

A spectral set, or set of spectral synthesis, for a commutative Banach algebra 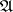is a closed subset of the space of maximal ideals 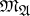which is the hull of exactly one closed ideal 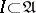. In the case when 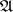is the group algebra of a locally compact Abelian group, spectral sets are also called sets of harmonic synthesis.

References

[1]	J. von Neumann, "Eine Spektraltheorie für allgemeine Operatoren eines unitären Raumes" Math. Nachr. , 4 (1951) pp. 258–281
[2]	V.E. Katznelson, V.I. Matsaev, Teor. Funkts. Funktsional. Anal. i Prilozhen. , 3 (1966) pp. 3–10

Comments

Cf. also Spectral synthesis.