Contingent

of a subset 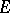of a Euclidean space at a point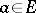

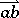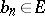The union of rays with origin for which there exists a sequence of points converging to such that the sequence of rays 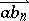converges to 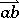. It is denoted by 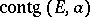. For an 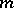-dimensional differentiable manifold 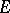, 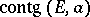is the same as the 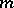-dimensional tangent plane to 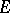at . This concept proves useful in the study of differentiability properties of functions. If for every point of a set 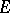in the plane, 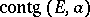is not the whole plane, then 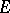can be partitioned into a countable number of parts situated on rectifiable curves. This theorem has been repeatedly generalized and refined. For example, a set of finite Hausdorff 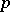-measure, 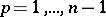, located in an -dimensional Euclidean space partitions into a countable number of parts, one of which has zero Favard measure of order 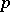, while each of the remaining parts is situated on some Lipschitz surface of dimension 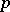; for almost-all 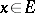(in the sense of the Hausdorff 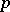-measure), 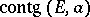is a plane of dimension 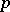if all variations of the set 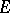are finite and, beginning with the 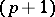-th, vanish.

References

[1]	G. Bouligand, "Introduction à la géometrie infinitésimale directe" , Vuibert (1932)
[2]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[3]	H. Federer, "Geometric measure theory" , Springer (1969)
[4]	L.D. Ivanov, "Variations of sets and functions" , Moscow (1975) (In Russian)

Comments

More on contingents (and the related notion of paratingent) can be found in G. Choquet's monograph [a1]. Contingents are useful in optimization problems nowadays.

References

[a1]	G. Choquet, "Outils topologiques et métriques de l'analyse mathématiques" , Centre Docum. Univ. Paris (1969) (Rédigé par C. Mayer)
[a2]	J.P. Aubin, I. Ekeland, "Applied nonlinear analysis" , Wiley (Interscience) (1984)