Whitney decomposition
A continuum is a non-empty compact connected metric space. A hyperspace of a continuum  is a space whose elements are in a certain class of subsets of
is a space whose elements are in a certain class of subsets of  . The most common hyperspaces are:
. The most common hyperspaces are:
 , the set of subsets
, the set of subsets  that are closed and non-empty; and
that are closed and non-empty; and
 , the set of subsets
, the set of subsets 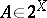 that are connected. Both sets are considered with the Hausdorff metric.
that are connected. Both sets are considered with the Hausdorff metric.
A Whitney mapping for  is a continuous function
is a continuous function  from
from  to the closed unit interval
to the closed unit interval  such that
such that  ,
, 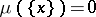 for each point
for each point 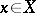 and, if
and, if  and
and  is a proper subset of
is a proper subset of 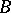 , then
, then  .
.
Every continuum admits Whitney mappings [a2], Thm. 13.4. These mappings are an important tool in the study of hyperspaces and they represent a way to give a "size" to the elements of 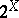 .
.
A Whitney level is a fibre of the restriction to 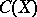 of a Whitney mapping for
of a Whitney mapping for  , that is, Whitney levels are sets of the form
, that is, Whitney levels are sets of the form  , where
, where 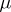 is a Whitney mapping for
is a Whitney mapping for  and
and  .
.
It is possible to consider the notion of Whitney level for  ; these have not been very interesting, mainly because they are not necessarily connected [a2], Thm. 24.2.
; these have not been very interesting, mainly because they are not necessarily connected [a2], Thm. 24.2.
In the case of  , Whitney levels are always compact and connected [a2], Thm. 19.9, and they have many similarities with the continuum
, Whitney levels are always compact and connected [a2], Thm. 19.9, and they have many similarities with the continuum  (see [a2], Chap. VIII, for these similarities).
(see [a2], Chap. VIII, for these similarities).
Furthermore, given a fixed Whitney mapping  , the set
, the set  is a very nice (continuous) decomposition of the hyperspace
is a very nice (continuous) decomposition of the hyperspace  . A set of this form is called a Whitney decomposition.
. A set of this form is called a Whitney decomposition.
A Whitney decomposition can be considered as an element of the hyperspace (of second order)  ; then it is possible to consider the space of Whitney decompositions,
; then it is possible to consider the space of Whitney decompositions,  . In [a1] it was proved that for every continuum
. In [a1] it was proved that for every continuum  ,
,  is homeomorphic to the Hilbert linear space
is homeomorphic to the Hilbert linear space  .
.
References
| [a1] | A. Illanes, "The space of Whitney decompositions" Ann. Inst. Mat. Univ. Nac. Autónoma México , 28 (1988) pp. 47–61 |
| [a2] | A. Illanes, S.B. Nadler Jr., "Hyperspaces, fundamentals and recent advances" , Monogr. Textbooks Pure Appl. Math. , 216 , M. Dekker (1999) |
Whitney decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitney_decomposition&oldid=43557