Binate group

A group 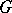in which every finitely-generated subgroup 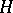(cf. also Finitely-generated group) admits a homomorphism 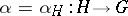and an element 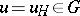such that for all ,

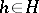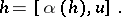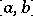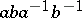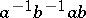(Here, the commutator may be taken to mean either or .) Thus, the subgroup 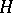is imbedded in 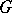both by 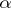and by inclusion. Such groups 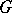are also called pseudo-mitotic [a4]. Every binate group is both infinitely generated and an acyclic group. This fact seems to be involved in most proofs of acyclicity of presently known acyclic groups [a2]. Existentially closed groups are binate. Every group is a normal subgroup of a normal subgroup of a binate group.

The structure of binate groups is revealed by the study of a binate tower, i.e., a chain of groups 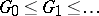, homomorphisms 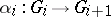and non-trivial structure elements 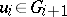subject to relations of the above form. There is a universal binate tower 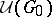, obtained from 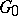by a sequence of HNN-extensions, with the characteristic property that every binate tower with base 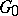admits a unique smallest sub-binate tower, and this is a quotient binate tower of in a unique way [a3]. In particular, the group 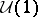is highly non-Hopfian and non-co-Hopfian (cf. also Hopf group). Its properties allow one to prove that binate groups admit no non-trivial finite-dimensional linear representation over any field [a1], and similarly for many acyclic groups of automorphisms [a5], [a6].

References

[a1]	R.C. Alperin, A.J. Berrick, "Linear representations of binate groups" J. Pure Appl. Algebra , 94 (1994) pp. 17–23
[a2]	A.J. Berrick, "Universal groups, binate groups and acyclicity" , Proc. 1987 Singapore Group Theory Conf. , W. de Gruyter (1989)
[a3]	A.J. Berrick, K. Varadarajan, "Binate towers of groups" Arch. Math. , 62 (1994) pp. 97–111
[a4]	K. Varadarajan, "Pseudo-mitotic groups" J. Pure Appl. Algebra , 37 (1985) pp. 205–213
[a5]	A.J. Berrick, "Groups with no nontrivial linear representations" Bull. Austral. Math. Soc. , 50 (1994) pp. 1–11
[a6]	A.J. Berrick, "Corrigenda: Groups with no nontrivial linear representations" Bull. Austral. Math. Soc. , 52 (1995) pp. 345–346