Courant theorem

on conformal mapping of domains with variable boundaries

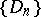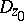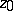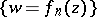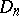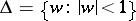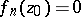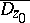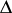Let be a sequence of nested simply-connected domains in the complex -plane, , which converges to its kernel relative to some point ; the set is assumed to be bounded by a Jordan curve. Then the sequence of functions which map conformally onto the disc , , , is uniformly convergent in the closed domain to the function which maps conformally onto , moreover , .

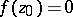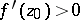This theorem, due to R. Courant , is an extension of the Carathéodory theorem.

References

[1a]	R. Courant, Gott. Nachr. (1914) pp. 101–109
[1b]	R. Courant, Gott. Nachr. (1922) pp. 69–70
[2]	A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) (Translated from Russian)

Comments

Cf. Carathéodory theorem for the definition of "kernel of a sequence of domains" .