Bicharacteristic

bicharacteristic strip, of a linear partial differential operator

A line of tangency of any two characteristics (cf. Characteristic)

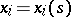of this linear partial differential operator. If the parameter is introduced on the bicharacteristic strip, then its equations , , are defined by solving a system of 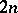ordinary differential equations

(*)

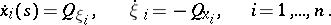Here is the principal symbol of the linear partial differential operator, the dot indicates differentiation with respect to the parameter and, if 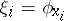, the equation 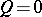is the characteristic equation of the differential operator. Thus, the solution 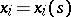, , 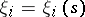, 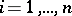of the system (*) for 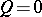defines the bicharacteristic strip 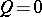. This bicharacteristic strip belongs to the characteristic 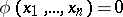, i.e. 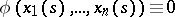, if the equations

and

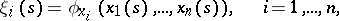are valid for at least one value of , then it follows that they are valid for all values of .

References

[1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)

Comments

The projections 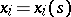, , 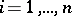into -space are called the bicharacteristic curves (or rays). The bicharacteristic curves are tangent to the characteristic hypersurfaces 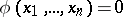due to the homogeneity of the principal symbol, as a function of 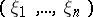, of degree equal to the order of the linear partial differential operator (cf. also Principal part of a differential operator; Symbol of an operator).

Nowadays, the standard reference on these matters is [a1], or the older, more concise, [a2].

References

[a1]	L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) pp. 271; 302
[a2]	L. Hörmander, "Linear partial differential operators" , Springer (1963) pp. 29; 31