Kepler equation

A transcendental equation of the form

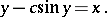The case 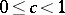is important for applications; here 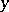is uniquely determined from a given and . This equation was first considered by J. Kepler (1609) in connection with the problem of planetary motion: Let the ellipse 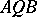(see Fig.) with focal point 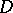be a planetary orbit, with circumscribed circle .

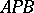Figure: k055210a

Then the Kepler equation gives the relation between the eccentric anomaly 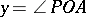and the mean anomaly , being the eccentricity of the ellipse.

The Kepler equation plays an important role in astronomy in determining the sections of elliptic orbits of planets.

References

[1]	M.F. Subbotin, "A course in celestial mechanics" , 1 , Leningrad-Moscow (1941) (In Russian)

Comments

The mean anomaly is a linear function of the time of the planet's passage at the point 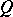. For more details, including the corresponding equations for hyperbolic and parabolic motion, see e.g. [a1].

References

[a1]	P.M. Fitzpatrick, "Principles of celestial mechanics" , Acad. Press (1970)